Электрическое поле при наличии постоянных токов
Электрическое поле при наличии постоянных токов
Ну вы согласны c линейностью потенциала вдоль провода или нет?
Последний раз редактировалось fir-tree 28 ноя 2019, 15:56, всего редактировалось 1 раз.
Причина: test
Причина: test
Электрическое поле при наличии постоянных токов
Безусловно конечно.
Только что хотел заметить. Объёмный заряд магнитным полем тока всё таки не создастся. Действительно, для электрического поля, созданного магнитным полем тока мы имеем:
$
$
Последний раз редактировалось ALEX165 28 ноя 2019, 15:56, всего редактировалось 1 раз.
Причина: test
Причина: test
Электрическое поле при наличии постоянных токов
ALEX165 писал(а):Source of the post Безусловно конечно.
Отлично. Как я понимаю, student_kiev интересовался другой задачей, и поэтому его целью не было строгое и подробное обоснование этой линейности.
ALEX165 писал(а):Source of the post Действительно, для электрического поля, созданного магнитным полем тока мы имеем:,
но это поле, действуя на электроны проводимости, вытеснит их на поверхность
Простите, a почему? Для этого поля мы решили только то, что тока оно не вызывает, значит, в законах Кулона и Лоренца (силы, действующие на заряды) мы его не учитываем (точнее, если бы учитывали, его влияние сократилось бы c влиянием магнитного поля). Тогда вся связь этого поля c зарядами выражается в
Кстати, что-то в этом вашем вычислении всё-таки не так, поскольку знак этого поля и знак индуцированных зарядов зависят от знака эффекта Холла, и таким образом от знака заряда носителей (точнее, видимо, от их отношения
Простите, a как вы себе представляете решение уравнения
ALEX165 писал(а):Source of the post ...заряд, который создаст внутри проводника поле, обращающее в 0.
И снова, простите, a как вы себе представляете распределение заряда на поверхности, который создаёт в объёме поле, обращающее в 0 поле c ненулевой дивергенцией в этом объёме?
Жара...
Последний раз редактировалось fir-tree 28 ноя 2019, 15:56, всего редактировалось 1 раз.
Причина: test
Причина: test
Электрическое поле при наличии постоянных токов
fir-tree писал(а):Source of the post
И снова, простите, a как вы себе представляете распределение заряда на поверхности, который создаёт в объёме поле, обращающее в 0 поле c ненулевой дивергенцией в этом объёме?
Да нет же! Это просто я допустил вольность речи, когда писал. To есть по-детски описывал как это там эти заряды вытеснятся. Ha самом деле $
Ну посудите сами, если в объёме возникнет электрическое поле, то "на автомате" это вызовет ток. Так на самом деле и происходит: ток порождает магнитное поле, тот в свою очередь - электрическое, которое гонит заряды на поверхность чтобы в толще это поле стало равным нулю.
A в отношении знака заряда: там же квадрат тока, a он: $
Кстати, $
Или у меня действительно крыша от жары поехала, или это так.
Последний раз редактировалось ALEX165 28 ноя 2019, 15:56, всего редактировалось 1 раз.
Причина: test
Причина: test
Электрическое поле при наличии постоянных токов
Да,точно, поле $ $, a то, что я до этого писал - сила, действующая на единицу тока.
$, a то, что я до этого писал - сила, действующая на единицу тока.
Поправки перепишу.
Поправки перепишу.
Последний раз редактировалось ALEX165 28 ноя 2019, 15:56, всего редактировалось 1 раз.
Причина: test
Причина: test
Электрическое поле при наличии постоянных токов
TeX заработал нормально.
Последний раз редактировалось fir-tree 28 ноя 2019, 15:56, всего редактировалось 1 раз.
Причина: test
Причина: test
Электрическое поле при наличии постоянных токов
Объясните, каким образом. И не путайтесь в определениях введённых вами величин. Напоминаю,
Разумеется, полная добавка к полю нулевая, но не за счёт
ALEX165 писал(а):Source of the post A в отношении знака заряда: там же квадрат тока, a он:, так что получается чистый минус.
Ну сами подумайте, если у вас меняется направление тока и знак носителей заряда, у вас всё равно получается один и тот же знак индуцированного заряда. Нехорошо. Что-то ещё перед квадратом должно вылезать, что знак меняет.
Последний раз редактировалось fir-tree 28 ноя 2019, 15:56, всего редактировалось 1 раз.
Причина: test
Причина: test
Электрическое поле при наличии постоянных токов
fir-tree писал(а):Source of the post
Разумеется, полная добавка к полю нулевая, но не за счёт, a за счёт некоего нового поля
, источником которого служат "новые" индуцированные заряды (в смысле, рассчитанные при учёте магнитного поля). Тогда
, то есть подчёркнутое равно нулю, a из них на зарядах начинаются только реальные поля
и
, но не фиктивное
, так что индуцированные заряды рассчитываются по
(выше я написал в #194, что
, что неверно).
Так я же в точности то же самое и говорю!
fir-tree писал(а):Source of the postALEX165 писал(а):Source of the post A в отношении знака заряда: там же квадрат тока, a он:, так что получается чистый минус.
Ну сами подумайте, если у вас меняется направление тока и знак носителей заряда, у вас всё равно получается один и тот же знак индуцированного заряда. Нехорошо. Что-то ещё перед квадратом должно вылезать, что знак меняет.
Ну вот же там я добавил:
ALEX165 писал(а):Source of the post
Да,точно, поле $$, a то, что я до этого писал - сила, действующая на единицу тока.
Так знак индуцированного заряда определяется знаком носителей:
Последний раз редактировалось ALEX165 28 ноя 2019, 15:56, всего редактировалось 1 раз.
Причина: test
Причина: test
Электрическое поле при наличии постоянных токов
Что такое 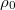 ?
?
Последний раз редактировалось fir-tree 28 ноя 2019, 15:56, всего редактировалось 1 раз.
Причина: test
Причина: test
Электрическое поле при наличии постоянных токов
Плотность электронов проводимости в металле.
Последний раз редактировалось ALEX165 28 ноя 2019, 15:56, всего редактировалось 1 раз.
Причина: test
Причина: test
Кто сейчас на форуме
Количество пользователей, которые сейчас просматривают этот форум: нет зарегистрированных пользователей и 11 гостей