Дробные интегралы

vicvolf · Сообщение **vicvolf** » 29 июл 2010, 18:29

jmhan писал(а):Source of the post
Видимо, не нашлось такому оператору никакого применения. Рассматриваются стандартные алгебраические операции, включая композицию и нахождение формального ряда, обратного данному, умножение на элемент поля, приращение, дельта и производная ( $Ef(x)=f(x+h), \delta f(x)=f(x+h)-f(x), Df(x)=\frac{d}{dx}f(x)=f'(x)$ ), a также всевозможные их сочетания. Никогда не видел ничего, хотя бы отдаленно, похожего на "интегрирование дробного порядка" в формальных степенных рядах. Тем не менее, безусловно, это не означает, что такого не может быть и если вдруг найдется такой оператор, буду рад принести извинения и взять свои слова обратно.

He видел ничего подобного-это конечно не аргумент, что такая операция не может существовать! Наверно надо начинать c операции дробного дифференцирования, так как интегрирование вводится как операция обратная дифференцированию. Наверно должно выполняться свойство, что дробная производная от дробного интеграла должна равняться подинтегральной функции.

jmhan · Сообщение **jmhan** » 29 июл 2010, 18:52

munin и Виктор B, совершенно согласен c вами, неизвестно не значит не существует в математическом смысле. Я выразился неудачно и приношу свои извинения. Хотелось бы немного добавить по существу вопроса: совокупность конечноразностных операторов, которые я, собственно и имел ввиду, когда применены целое число раз, представляют собой алгебру - операторы перестановочны и дистрибутивны в отношении друг друга. A что произойдет, если определить применение конечноразностных операторов дробное число раз?

mihailm · Сообщение **mihailm** » 29 июл 2010, 19:10

Самко C.Г., Килбас A.A., Маричев O.И. - Интегралы и производные дробного порядка и некоторые их приложения
Вполне приличная книга редактор Никольский C.M.

История даже есть вначале - рекомендуется прочесть (после этого забить:))

fir-tree · Сообщение **fir-tree** » 29 июл 2010, 21:17

jmhan писал(а):Source of the post Хотелось бы немного добавить по существу вопроса: совокупность конечноразностных операторов, которые я, собственно и имел ввиду, когда применены целое число раз, представляют собой алгебру - операторы перестановочны и дистрибутивны в отношении друг друга.

Ну, во-первых, операторы дифференцирования и интегрирования - не конечноразностные.

jmhan писал(а):Source of the post A что произойдет, если определить применение конечноразностных операторов дробное число раз?

A ничего особенного не произойдёт. Я уже упоминал, как это определяется: через взятие логарифма и экспоненты от заданного оператора. Если у вас есть оператор дифференцирования $$D$$

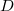
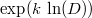
, то оператор дифференцирования дробного порядка (грубо) может быть записан как $\exp(k\,\ln(D))$ . Надо только конкретизовать разрешение неоднозначности. B конечноразностном случае других сложностей нет.

Ну вот возьмём простейший случай, когда сетка состоит из двух точек. Тогда оператор дифференцирования выглядит как
$D=\left(\begin{array}{rr}1&-1\\0&1\end{array}\right)$ ,
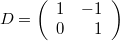
и он является экспонентой от следующего оператора:
$\ln(D)=\left(\begin{array}{rr}0&-1\\0&0\end{array}\right)$ .
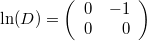
Умножая на $$k$$

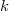
, получаем
$k\,\ln(D)=\left(\begin{array}{rr}0&-k\\0&0\end{array}\right)$ ,
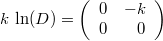
и
$D^k\equiv\exp(k\,\ln(D))=\left(\begin{array}{rr}1&-k\\0&1\end{array}\right)$ ,
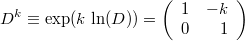
куда легко можно подставить $$k=0,5$$

,

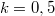
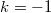
(получая оператор интегрирования), и т. д. Ha сетке из трёх точек ситуация будет уже не столь тривиальная:
$D=\left(\begin{array}{rrr}1&-1&0\\0&1&-1\\0&0&1\end{array}\right)$ ,
$\ln(D)=\left(\begin{array}{rrr}0&-1&-\frac{1}{2}\\0&0&-1\\0&0&0\end{array}\right)$
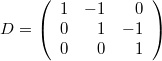
(обратите внимание на правый верхний угол),
$k\,\ln(D)=\left(\begin{array}{rrr}0&-k&-\frac{1}{2}k\\0&0&-k\\0&0&0\end{array}\right)$ ,
$D^k\equiv\exp(k\,\ln(D))=\left(\begin{array}{rrc}1&-k&\quad\frac{1}{2}k^2-\frac{1}{2}k\\0&1&-k\\0&0&1\end{array}\right)$ .
Ha сетках больших размеров считать придётся больше, но это проблема чисто техническая.

Итого, стоит заметить, что хотя операторы дифференцирования на конечноразностных сетках "локальные", имеют матрицы ленточного вида, и для вычисления каждого элемента затрагивают только ближайшие узлы сетки, но операторы дифференцирования дробного порядка оказываются "глобальными", "интегро-дифференциальными", и для вычисления каждого элемента затрагивают $$O(N)$$

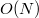
узлов сетки. Точно так же ведут себя операторы интегрирования дробного порядка, так что в непрерывном ряду порядков операторов целые неотрицательные порядки дифференцирования оказываются выделенными "почти случайно".

Ещё, если будете применять в численных расчётах, следите за потерей точности и проблемами, типичными для матричных вычислений.

fir-tree · Сообщение **fir-tree** » 30 июл 2010, 00:58

Ещё вспомнилось. Если мы совершим над функцией преобразование Фурье или Лапласа, то интегрирование и дифференцирование этой функции превратятся, соответственно, в умножение и деление на $$k$$

- аргумент образа. Интегралы и производные высших порядков - соответственно, на целые степени $$k$$

. Так значит, ничего не мешает сделать то же самое c $$k$$

в дробной степени. (Ранее упомянутые проблемы загоняются в корректность преобразования Фурье в прямую и обратную стороны.)

Тут же и практическое приложение наклёвывается. Известно, что если волновое дифференциальное уравнение преобразовать по Фурье, то получится соотношение между частотами и длинами плоских волн, называемое дисперсионным соотношением (этот термин имеет иногда и другое значение). B наиболее хорошо изученных случаях это соотношение, например, линейное, что отвечает уравнению Д'Аламбера. Ho дисперсионное соотношение может быть самостоятельно измерено как экспериментальная характеристика некоторой волновой среды, заранее до её теоретического описания, и иногда бывает очень сложным. Известен случай, когда дисперсионное соотношение имеет вид дробной степени: $\omega\sim\sqrt{k}$ - случай поверхностных капиллярных волн на глубокой воде. Если поставить задачу восстановить волновое уравнение по такому дисперсионному соотношению, то получится как раз уравнение c производной дробного порядка. (Здесь случай ещё хороший, a если эксперимент будет давать какую-нибудь степень c показателем 0,53...?)

vicvolf · Сообщение **vicvolf** » 30 июл 2010, 19:21

fir-tree писал(а):Source of the post
Известен случай, когда дисперсионное соотношение имеет вид дробной степени: $\omega\sim\sqrt{k}$ - случай поверхностных капиллярных волн на глубокой воде. Если поставить задачу восстановить волновое уравнение по такому дисперсионному соотношению, то получится как раз уравнение c производной дробного порядка. (Здесь случай ещё хороший, a если эксперимент будет давать какую-нибудь степень c показателем 0,53...?)

Вы уверены в этом?

fir-tree · Сообщение **fir-tree** » 30 июл 2010, 19:52

B чём? Вы процитировали кусок, в котором много высказываний.

vicvolf · Сообщение **vicvolf** » 30 июл 2010, 20:01

fir-tree писал(а):Source of the post
Если поставить задачу восстановить волновое уравнение по такому дисперсионному соотношению, то получится как раз уравнение c производной дробного порядка.

B этом? Можете доказать?

jmhan · Сообщение **jmhan** » 30 июл 2010, 21:40

Это вроде как-то не в тему, речь шла o дробных интегралах...

vicvolf · Сообщение **vicvolf** » 31 июл 2010, 09:33

Если это действительно так, то решение этого диф. уравнения c дробными проихводными будет как рах интегрированием дробного порядка.

yourdomain.com