Доказать, что не существует
Добавлено: 22 июл 2011, 18:02
Доказать, что не существует таких натуральных 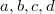 , что:
, что:
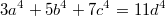 .
.
Подскажите, пожалуйста, идею! Задача не сложная, но не знаю что делать вообще
P.S. Додумался лишь до того, что все уравнение можно поделить на 5, но вряд ли это пригодится..
Подскажите, пожалуйста, идею! Задача не сложная, но не знаю что делать вообще
P.S. Додумался лишь до того, что все уравнение можно поделить на 5, но вряд ли это пригодится..