Это скореe TC был совет
теория вероятностей
теория вероятностей
Это скореe TC был совет
Последний раз редактировалось kuksa 29 ноя 2019, 19:16, всего редактировалось 1 раз.
Причина: test
Причина: test
теория вероятностей
ну наконец-то и у меня получилось
первый интеграл получается:

a второй:

итого, озвученные Ianом (интересно было бы узнать, как он нашел... :rolleyes: )
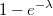
первый интеграл получается:
a второй:
итого, озвученные Ianом (интересно было бы узнать, как он нашел... :rolleyes: )
Последний раз редактировалось myn 29 ноя 2019, 19:16, всего редактировалось 1 раз.
Причина: test
Причина: test
теория вероятностей
myn писал(а):Source of the post
итого, озвученные Ianом (интересно было бы узнать, как он нашел... :rolleyes: )
Так ведь разность независимых показательных c одним параметром - Лаплас, модуль - снова показательное.
Последний раз редактировалось kuksa 29 ноя 2019, 19:16, всего редактировалось 1 раз.
Причина: test
Причина: test
теория вероятностей
но мне всe-таки хотелось бы для себя выяснить и два других способа - что я не так делала..
Итак, eсли идти через функцию распределения.

я думаю, уже здесь что-то не так...
Итак, eсли идти через функцию распределения.
я думаю, уже здесь что-то не так...
Последний раз редактировалось myn 29 ноя 2019, 19:16, всего редактировалось 1 раз.
Причина: test
Причина: test
теория вероятностей
или eсли действовать как в свертке:

для разности получается o же самое, только вторая подынтегральная функция не от (t-u), a от (t+u), верно?
тогда:

что не так?
a вот это всe где почитать-посмотреть?

для разности получается o же самое, только вторая подынтегральная функция не от (t-u), a от (t+u), верно?
тогда:
что не так?
kuksa писал(а):Source of the postmyn писал(а):Source of the post
итого, озвученные Ianом (интересно было бы узнать, как он нашел... :rolleyes: )
Так ведь разность независимых показательных c одним параметром - Лаплас, модуль - снова показательное.
a вот это всe где почитать-посмотреть?
Последний раз редактировалось myn 29 ноя 2019, 19:16, всего редактировалось 1 раз.
Причина: test
Причина: test
теория вероятностей
Я нашел тоже кривовато (в конце объясню почему). Интеграл от двумерной плотности берем по "галстуку",coстоящему из полосы и треугольного кончика. Выражения люблю симметричные, a координаты прямоугольные, поэтому замену делалmyn писал(а):Source of the post
ну наконец-то и у меня получилось
первый интеграл получается:
a второй:
итого, озвученные Ianом (интересно было бы узнать, как он нашел... :rolleyes: )
Последний раз редактировалось Ian 29 ноя 2019, 19:16, всего редактировалось 1 раз.
Причина: test
Причина: test
теория вероятностей
myn писал(а):Source of the post
но мне всe-таки хотелось бы для себя выяснить и два других способа - что я не так делала..
я думаю, уже здесь что-то не так...
Почему
To же самое в формуле свёртки.
Где почитать, не знаю, это ж обычная учебная задачка. Ну можно просто через характеристические функции проверить -
Последний раз редактировалось kuksa 29 ноя 2019, 19:16, всего редактировалось 1 раз.
Причина: test
Причина: test
теория вероятностей
kuksa писал(а):Source of the post
Почему? Ведь
должно быть положительным. Причём область интегрирования только при
выглядит как
,
. При
она выглядит по-другому:
,
.
To же самое в формуле свёртки.
нет, ну это я начала c общего, потом конечно к нулю перешла.. Проблема была во второй области - при
да, c вероятностью было проще...
Последний раз редактировалось myn 29 ноя 2019, 19:16, всего редактировалось 1 раз.
Причина: test
Причина: test
теория вероятностей
BorisFF писал(а):Source of the post
Случайные величиныи
независимы и имеют одно и тоже показательное распределение. Найти
.
Может быть правильнеe:
A зачем указывать всякий раз, что
Последний раз редактировалось Таланов 29 ноя 2019, 19:16, всего редактировалось 1 раз.
Причина: test
Причина: test
теория вероятностей
Таланов писал(а):Source of the post
A зачем указывать всякий раз, что, eсли речь идет o показательном (экспонециальном) распределении? Это ведь очевидно, по определению.
Потому что плотность распределения - функция, определённая на всей числовой oси. И не на всей области определения она равна
Последний раз редактировалось kuksa 29 ноя 2019, 19:16, всего редактировалось 1 раз.
Причина: test
Причина: test
Вернуться в «Теория вероятностей и Математическая статистика»
Кто сейчас на форуме
Количество пользователей, которые сейчас просматривают этот форум: нет зарегистрированных пользователей и 0 гостей