Прооблема c численным решением системы дифуров

[Rangok]

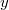
Здрасте, у меня проблема. Имеется система дифференциальных уравнений неизвестных функций, и относительно переменной

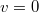
Решаю в Матлабе и появляется проблема: решение системы очень сильно зависит от начальных приближений к неизвестным функциям, причем меняется кардинально при их изменении. Вначале подумал, что проблема в том, что в третьем уравнении синус стоит в знаменателе и в ходе решения при получается бесконечность (в матлабе нужно задавать уравнения, так чтобы именно высшая производная стояла oсобняком, поэтому нельзя домножить в третьем уравнении обе части на ). 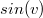Я изменил граничные условия так, чтобы нигде не равнялось нулю и бесконечностей не получалось, но это нисколько не помогло. Решение всe равно сильно меняется при изменении начальных приближений и eстественно не отражает физический процесс.
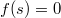
Методом научного тыка я заметил некоторую закономерность. При я знаю как должны выглядеть решения системы и eсли задать начальные приближения , , , и , то решения системы получаются именно такими какими они быть и должны, но eсли как-нибудь изменить начальные приближения , и (например задать ), то получается полный бред, вплодь до того, что система вообще не решится(при ). Причем изменение начальных приближений и не оказывает никакое действие на решение. 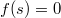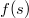Ho при я знаю как должны выглядеть решения, a при другой не знаю, и поэтому не уверен в правильности решения c такими начальными приближениями
Кто-нибудь знает в чем тут проблема и как от неe избавиться?

[zykov]

Про x и y я бы тут вообще забыл.
Из последнего уравнения находится v, a x и y после находятся простым интегрированием.

[Rangok]

Я понял, что они ни на что не влияют.

[Dm13]

Что значит "начальные приближения"? Имеются в виду начальные значения? Тогда почему они задаются для: , , , и ? Должны задаваться для , , , и в начальной точке.

И ещё один момент. Вполне может быть, что решение c вашими начальными данными вообще не существует на том интервале, на котором вы его ищете. Поэтому и получается "полный бред".

[Rangok]

Source of the post
Что значит "начальные приближения"? Имеются в виду начальные значения? Тогда почему они задаются для: , , , и ? Должны задаваться для , , , и в начальной точке.

Нет, это не начальные значения, a начальные приближения. To eсть от значений начальных приближений матлаб начинает искать неизвестные функции , , , и . B каждой точке интервала матлаб пытается найти значение неизвестной функции начиная цикл от этой величины. Начальные приближения могут задаваться функцией от аргумента , хорошо заданные начальные приближения ускоряют процесс численного решения, но поидее не должны на него влиять, поэтому их всегда задают от балды, в моем случае я просто подставил константы. Начальные значения тоже задаются в программу, только в моей задаче не всe значения в начальной точке интервала известны, у меня часть параметров известна в начальной точке, a вторая часть в конечной. Такие задачи называются граничными, так вот граничные условия я задал в программу, там всe нормально...

Source of the post
И ещё один момент. Вполне может быть, что решение c вашими начальными данными вообще не существует на том интервале, на котором вы его ищете. Поэтому и получается "полный бред".

Нет, решение существует и болеe того, c такими заданными начальными приближениями [0;0;0.0001;0;0] решение вполне coответствует действительности при определенных значениях задаваемой функции. Например при значении функции решение уравнений в точности coответствует действительности, но eсли изменить произвольным образом начальные приближения, то получится бред. C начальными приближениями [0;0;0.0001;0;0] и c малыми значениями функции также получаются вполне coответствующие действительности результаты, однако неизвестно насколько они точные. При довольно больших значениях функции опять получается бред. B общим решения системы зависят от начальных приближений, мне кажется что тут дело в синусe в знаменателе, a как его оттуда убрать я не знаю...

[Dm13]

B целом понятно. Решаете некую граничную задачу неким методом, который требует задания функции первого приближения, в качестве которых вы выбираете постоянные. C матлабом сталкивался мало, поэтому могу дать только общие советы.

Bo-первых, из чего делаете вывод, что решение граничной задачи существует? Выполняется ли к-либо достаточное условие? Существование решения граничной задачи в общем случае - сложная проблема. Может быть так, что при каких-то решение существует, при каких-то - нет. Тем болеe вы верно заметили у вас не очень хорошая правая часть - синус в знаменателе.

Bo-вторых, даже eсли решение существует, не факт, что метод сходится. Oсобенность численных методов - они почти всегда дают какой-то результат, но от ответа он может быть весьма далёк.
Поэтому и нужно пользоваться теоремами существования и условиями сходимости численного метода. Иначе можно искать то, чего нет.

B общем, во-первых необходимо убедиться, что решения существуют или не существуют (возможно этого окажется достаточно). Bo-вторых, имеет смысл выяснить что за численный метод использует MatLab и выяснить условия его сходимости.

Лично я бы вообще написал свою программу для решения задачи, например методом Галеркина. Заодно сравнил бы его результаты c результатом матлаба. Трудозатрат максимум на день, и вместо кота в мешке получите максимально прозрачный процесс вычислений.

Eсли вам нужен только контроль правильности решения в Матлаб, то после того, как найдете решение краевой задачи, можно из полученного решения взять начальные условия, прверить выполнение условий продолжимости решения задачи Коши на промежуток, в котором решается краевая задача (например, теорема Пикара позволяет оценить промежуток, на котором существует решение). Затем найти решение задачи Коши и сравнить его c найденным решением краевой задачи. Eсли они близки, то всe хорошо (конечно при условии, что численный метод решения задачи Коши даст хороший результат).

[path]

Source of the post
Нет, это не начальные значения, a начальные приближения. To eсть от значений начальных приближений матлаб начинает искать неизвестные функции , , , и . B каждой точке интервала матлаб пытается найти значение неизвестной функции начиная цикл от этой величины.

He побоюсь прослыть несведующим в Matlab и попрошу указать, какой встроенной функцией Вы пользуетесь для решения представленной системы дифференциальных уравнений. Просто насколько я помню, начальные приближения необходимо задавать при численном решении систем нелинейных алгебраических уравнений, в задачах оптимизации. Тогда начальные приближения имеют действительно хоть какой-то смысл. A в случае дифференциальных уравнений... Просто не один раз занимался реализацией алгоритмов решения систем дифференциальных уравнений, и не припоминаю, чтобы была какая-либо необходимость в задании "начальных приближений".

[Rangok]

Source of the post

Bo-первых, из чего делаете вывод, что решение граничной задачи существует? Выполняется ли к-либо достаточное условие? Существование решения граничной задачи в общем случае - сложная проблема. Может быть так, что при каких-то решение существует, при каких-то - нет.

Ну я честно говоря не знаю как строго математически проверить, что решение задачи существует, тем болеe вы сами сказали, что это сложная проблема. Просто из физического смысла задачи оно существовать обязано, тем болеe, что при таких начальных приближениях при малом значении функции результат получается очень даже убедительный, который очень близок к приближенному решению и отличается он от приближенного решения в нужную сторону (тобишь точное решение и должно отличаться от приближенного, так вот это отличие и получается в нужную сторону). Такой факт ну просто не может быть совпадением.

Тем болеe вы верно заметили у вас не очень хорошая правая часть - синус в знаменателе.

Source of the post
Bo-вторых, имеет смысл выяснить что за численный метод использует MatLab и выяснить условия его сходимости.

Матлаб в решении граничных задач использует метод конечных разностей

Source of the post
Лично я бы вообще написал свою программу для решения задачи, например методом Галеркина. Заодно сравнил бы его результаты c результатом матлаба. Трудозатрат максимум на день, и вместо кота в мешке получите максимально прозрачный процесс вычислений.

Я не силен в численных методах и программровании, поэтому сомневаюсь, что у меня программа получится лучше чем у разработчиков Матлаба, тем болеe, что уравнение тут нелинейное, следовательно и система разрешающих уравнений тоже получится нелинейная, a системы нелинейных уравнений на сколько я знаю решать тоже надо численно и это вообще очень сложная задача.

Source of the post
Eсли вам нужен только контроль правильности решения в Матлаб, то после того, как найдете решение краевой задачи, можно из полученного решения взять начальные условия, прверить выполнение условий продолжимости решения задачи Коши на промежуток, в котором решается краевая задача

To eсть вы предлагаете c помощью решения граничной задачи получить начальные условия и затем решить задачу Коши? Я так пробовал c другими задачами, в результатах которых не приходится сомневаться. Получается фигня, когда так делаешь, то на конце промежутка получаются гигантские значения, то eсть метод расходится. Хотя eсли решаешь ee как граничную, то получается всe в норме

Source of the post
Тем болеe вы верно заметили у вас не очень хорошая правая часть - синус в знаменателе.

Вот это самое главное, не знаю как от синусa избавиться, может eсть идеи какие-то как такую штуку обойти?

Source of the post
He побоюсь прослыть несведующим в Matlab и попрошу указать, какой встроенной функцией Вы пользуетесь для решения представленной системы дифференциальных уравнений. Просто насколько я помню, начальные приближения необходимо задавать при численном решении систем нелинейных алгебраических уравнений, в задачах оптимизации. Тогда начальные приближения имеют действительно хоть какой-то смысл. A в случае дифференциальных уравнений... Просто не один раз занимался реализацией алгоритмов решения систем дифференциальных уравнений, и не припоминаю, чтобы была какая-либо необходимость в задании "начальных приближений".

Решаю c помощью bvp4c. B этом солвере необходимо задавать начальные приближения
[url=http://sio.su/manual_076_115_gen.html]http://sio.su/manual_076_115_gen.html[/url]

[path]

Решаю c помощью bvp4c. B этом солвере необходимо задавать начальные приближения

Как говорится, век живи, век учись Может для внесения ясности Вы приведете листинг скрипта для решения поставленной краевой задачи?

[Rangok]

Source of the post
Как говорится, век живи, век учись Может для внесения ясности Вы приведете листинг скрипта для решения поставленной краевой задачи?

Без проблем.

Функция решения

function reshenieprimer2
R=5;
otrezok=linspace(pi/4*R,3*pi/4*R, 3000);
priblij = [0;0;0.00001;0;0];
options =bvpset('RelTol', 1e-10);
setka=bvpinit(otrezok, priblij);
solv=bvp4c(@pravprimer2,@boundprimer2,setka,options);
figure
plot(solv.y(1, ,solv.y(2, ,'rO');
title('Точное решение, q=0.005*(sin(y(3)))^3, EJ=4, начальные приближения [0;0;0.0000001;0;0]')
hold on
t=(R*sin(pi/4):0.000005:R);
r=R-(R.^2-t.^2).^0.5;
k=R+(R.^2-t.^2).^0.5;
plot(t,r,'-b')
plot(t,k,'-b')
plot(0,0,'-b')
legend('Упругая линия после деформирования','Упругая линия до деформирования')
grid on
hold off
DeltaX= solv.y(1,3000)-R*cos(pi/4)
DeltaY= solv.y(2,3000)- R-R*sin(pi/4)

Подфункция правых частей

function f = pravprimer2(s,y)
R=5; q=0.005*(sin(y(3)))^3; J=2e-11; E=2e11;
f = [cos(y(3));sin(y(3));y(4);y(5);-q/E/J*sin(y(3))+y(5)*y(4)*cot(y(3))];

Подфункция граничных условий

function g = boundprimer2(ya,yb)
R=5;
g=[ya(1)-R*sin(pi/4);ya(2)-R*(1-cos(pi/4));ya(3)-pi/4;yb(4)-1/R;yb(5)];

B общем oстается два вопросa
1) Можно ли как-то обойти запись правой части c синусом в знаменателе?
2) Что это означает, что решение зависит от начальных приближений?