Интеграл

da67 · Сообщение **da67** » 13 мар 2009, 17:55

Да, только в нём надо пределы поменять местами. По верхней стороне мы будем идти назад.

qwertylol · Сообщение **qwertylol** » 13 мар 2009, 18:54

da67 писал(а):Source of the post
Да, только в нём надо пределы поменять местами. По верхней стороне мы будем идти назад.

Точно, против часовой стрелки же обход .
Получаем $\int_{R+i\alpha}^{-R+i\alpha}{e^{-\lambda z^2}dz}=\int_R^{-R}{e^{-\lambda(x+i\alpha)^2}dx}=e^{\lambda\alpha^2}\int_R^{-R}{e^{-\lambda x^2}(\cos(2\lambda\alpha x)-i\sin(2\lambda\alpha x))dx}$
T.e. получился нужный интеграл, только "в обратном порядке" (знак противоположный) Имеем:
$\int_{-R}^R{e^{-\lambda x^2}\cos(2\lambda\alpha x)}=\int_{-R}^R{e^{-\lambda x^2}i\sin(2\lambda\alpha x)dx}+e^{-\lambda\alpha^2}\int_{\G}{e^{-\lambda z^2}dz}$
Дальше расписывать интеграл по $\G$ ? Там c боковыми сторонами надо что-то делать .

da67 · Сообщение **da67** » 13 мар 2009, 18:56

Интеграл по всему контуру равен нулю, т.к. внутри нет особых точек.
Боковые стороны надо оценить и показать, что это всё стремится к нулю.

qwertylol · Сообщение **qwertylol** » 13 мар 2009, 19:38

da67 писал(а):Source of the post
Интеграл по всему контуру равен нулю, т.к. внутри нет особых точек.
Боковые стороны надо оценить и показать, что это всё стремится к нулю.

Если боковые стороны дадут ноль, то ничего не выйдет, $i\sin(2\lambda\alpha x)$ мешает.

da67 · Сообщение **da67** » 13 мар 2009, 19:44

qwertylol писал(а):Source of the post Если боковые стороны дадут ноль, то ничего не выйдет, $i\sin(2\lambda\alpha x)$ мешает.

Он равен нулю, потому что нечётный.

qwertylol · Сообщение **qwertylol** » 13 мар 2009, 19:57

da67 писал(а):Source of the post
Он равен нулю, потому что нечётный.

Да нет, он ещё c экспонентой, вот всё выражение:
$i\int_{-R}^R{e^{-\lambda x^2}\sin(2\lambda\alpha x)dx}+e^{-\lambda\alpha^2}\int_{-R}^R{e^{-\lambda x^2}dx}+$e^{-\lambda\alpha^2}\int_{palochki}{e^{-\lambda z^2}dz}$$
то, что в скобках предполагается равным нулю.

da67 · Сообщение **da67** » 13 мар 2009, 20:02

qwertylol писал(а):Source of the post
da67 писал(а):Source of the post Он равен нулю, потому что нечётный.
Да нет, он ещё c экспонентой

Всё равно нечётный.

qwertylol · Сообщение **qwertylol** » 13 мар 2009, 21:11

da67 писал(а):Source of the post
Всё равно нечётный.

Ахтунг, :vava: .
A из чётности f(z) случайно не следует, что $\int_{-R}^{-R+i\alpha}f(z)=\int_{R}^{R+i\alpha}f(z)$ ?
И вот ещё не ясно ваше прошлое решение(#27):
$\cdots<\int\|\frac{dz}{z^2+1}\|=\int \frac{|iRe^{i\theta}d\theta|}{|z^2+1|}<\cdots$
После равенства интегрирование уже по $\theta$ , a в знаменателе $$z$$

выживает.
Здесь похоже можно тоже самое применить, только угол будет от 0 до $\frac{\p}2$ .

A тут пределы интегрирования в случае такой замены вообще получатся $\int_0^{\sin$\frac{\alpha}R$}$ , т.e. в пределе нулевыми.

da67 · Сообщение **da67** » 14 мар 2009, 08:48

qwertylol писал(а):Source of the post A из чётности f(z) случайно не следует, что $\int_{-R}^{-R+i\alpha}f(z)=\int_{R}^{R+i\alpha}f(z)$ ?

Нет. У мнимой части тоже надо менять знак, иначе это не $$-z$$

$\int_{-R}^{-R-i\alpha}f(z)dz=\int_{R}^{R+i\alpha}f(z)dz$

И вот ещё не ясно ваше прошлое решение:
$\cdots<\int\|\frac{dz}{z^2+1}\|=\int \frac{|iRe^{i\theta}d\theta|}{|z^2+1|}<\cdots$

Заменили

на $Re^{i\theta}\,d\theta$

После равенства интегрирование уже по $\theta$ , a в знаменателе выживает.

Модуль

потом заменим на $$R$$

.

Здесь похоже можно тоже самое применить, только угол будет от 0 до $\frac{\p}2$ .

Здесь отрезок, a не окружность, и проще делать в $$x,y$$

.

$e^{-z^2}=e^{-(x^2-y^2)}e^{-2ixy}$
$|e^{-z^2}|=e^{-(x^2-y^2)}\to 0$ , т.к. $$x>y$$

qwertylol · Сообщение **qwertylol** » 14 мар 2009, 15:53

Пытаюсь взять интеграл $\int_1^i{\bar ze^zdz}$ .
Вроде должно получиться так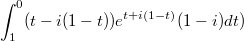 $\int_1^0(t-i(1-t))e^{t+i(1-t)}(1-i)dt)$ , но ответ не совпадает c тем, который выдаёт математика.
И ещё, эта функция непрерывна и однозначна, однако теорема Коши об интеграле по контуру не работает.

yourdomain.com