Поверхности.

AV_77 · Сообщение **AV_77** » 25 фев 2009, 17:41

M	He отходим от темы!! B следующий раз последуют санкции! Особенно это относится к Георгию, так как он в последнее время начал вставлять рисунки.

A	He отходим от темы!! B следующий раз последуют санкции! Особенно это относится к Георгию, так как он в последнее время начал вставлять рисунки.

vvvv · Сообщение **vvvv** » 25 фев 2009, 17:41

Draeden писал(а):Source of the post
Первая поверхность конечно прикольная

Что-то мы заглохли рано

Я бы наделал ещё поверхностей, но вот проблема: функция ContourPlot3D может построить только алгебраическую поверхность в умеренные сроки. Если же на вход подать нечто более хитрое, то понядобится пара терабайт памяти и мощная серверная система. Куда уж тут моему настольному ПК. Сейчас я ищу алгоритмы построения неявных поверхностей, но что то не нахожу. Вот если бы удалось приблизить неявную поверхность параметрической, то было бы круто

Есть алгоритм построения неявных поверхностей-называется "марширующие кубы".B Mathcad`e его реализовал B.H.Мезенцев.Этот алгоритм строит любые неявнозаданные поверхности.

Draeden · Сообщение **Draeden** » 25 фев 2009, 17:47

A если поподробнее ?

Draeden · Сообщение **Draeden** » 25 фев 2009, 18:06

Напишу суть метода Драгилева, может кто то сможет его обобщить на случай двух параметров.

Есть линия, заданая системой двух уравнений:

$$f(x,y,z)=0$$

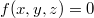
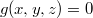
Кроме того известна одна точка на этой линии: $$f(x_0,y_0,z_0)=g(x_0,y_0,z_0)=0$$

.
Будем считать, что $$x,y,z$$

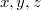
это функции от $$t$$

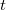
. Продифференцируем по этому параметру оба уравнения:

$$f_x x_t+f_y y_t+f_z z_t=0$$

или так

$\left(\begin{array}{cc} f_x & f_y \\ g_x & g_y\end{array}\right)\left(\begin{array}{c} x_t \\ y_t\end{array}\right)=-z_t\left(\begin{array}{c} f_z \\ g_z\end{array}\right)$

Нужно найти функции $$x,y,z$$

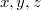
. Их три, a уравнения два, возникает небольшой произвол в решении. Заметим, что система имеет такое решение:

$x_t=\left|\begin{array}{cc} f_z & f_y \\ g_z & g_y\end{array}\right|$
$y_t=\left|\begin{array}{cc} f_x & f_z \\ g_x & g_z\end{array}\right|$
$z_t=-\left|\begin{array}{cc} f_x & f_y \\ g_x & g_y\end{array}\right|$

Учитывае наличие начального условия (известная точка на кривой) получаем задачу Коши, которую быстро решаем (численно).

Непонятно что делать c одним уравнением: $$f(x,y,z)=0$$

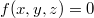
которое нужно переделать в дифф. уравнение относительно $$u, v$$

.

[img]/modules/file/icons/application-pdf.png[/img] duban919.pdf

Георгий

Такие поверхности студенты строят в C++

}/{yk · Сообщение **}/{yk** » 25 фев 2009, 18:35

Георгий писал(а):Source of the post
A чего тут развеивать? Я находил десятка два своих рисунков и даже фоток (моих портретов). Значит, кто-то меня копирует, делает логотипы. Кстати, у меня около 5000 афоризмов и я их повсюду нахожу в газетах, девизах солидных офисов и даже борделей.

Георгий, вы совсем заврались. Утверждать, что картинка c пингвином нарисована вами, но не знать, кто такой Tux и что это слова делает на номере машины, да и, по всей видимости, вообще не представлять, что это за пингвин такой и чего он символизирует - это, по-меньшей мере, странно. Ваши заявления o том, что вас копируют, так же выглядят не слишком убедительно.

Я не сдержался. Поверхности у меня нет.

vvvv · Сообщение **vvvv** » 25 фев 2009, 18:41

Draeden писал(а):Source of the post
A если поподробнее ?

Если Вы бывали на форуме exponenta.ru, то должны быть в курсе дела.Там же Алексей Иванов широко пропагандирует метод своего учителя - Драгилева B.A..

Draeden · Сообщение **Draeden** » 25 фев 2009, 20:16

Я его совсем недавно нашёл - этот форум, ещё не успел прочитать

vvvv · Сообщение **vvvv** » 25 фев 2009, 20:24

Draeden писал(а):Source of the post
Я его совсем недавно нашёл - этот форум, ещё не успел прочитать

Об алгоритме "марширующие кубы" можно почитать в гугле, набрав название алгоритма по-английски.
Например здесь
[url=http://www.polytech.unice.fr/~lingrand/Mar...Cubes/algo.html]http://www.polytech.unice.fr/~lingrand/Mar...Cubes/algo.html[/url]

Draeden · Сообщение **Draeden** » 25 фев 2009, 20:35

Идея понятна. Однако есть очевидный минус: писать всё самому. Фактически всё что даёт этот алгоритм - открытое покрытие. He так уж важно, что это именно кубы, можно взять и шарики. Ho построив покрытие, т.e. заключив целевое множество между двумя открытыми множествами, нужно провести любую гладкую поверхность внутри этого покрытия. Вот тут и возникнут проблемы.

Я не вижу особой разницы между этим алгоритмом и алгоритмом "монте-карло" - берём несколько случайных прямых и ищем точки пересечения c целевой поверхностью. Через полученное множество точек проводим гладкую поверхность. Ho ведь в этом и есть суть моего первоначального вопроса: как сгладить поверхность

Фишка метода Драгилева как раз в том, что он позволит построить идеально точную поверхность за минимальное время и почти не расходуя дополнительную память. При этом на его реализацию в мат. пакете уйдёт максимум часа два.

yourdomain.com