может и пройти.
численный ряд сходящийся
численный ряд сходящийся
Ho идея хорошая. Что-нибудь такое
![$$\sum \frac{e^{2i\pi n/3}}{\sqrt[3]{n}}$$ $$\sum \frac{e^{2i\pi n/3}}{\sqrt[3]{n}}$$](http://fx.ifz.ru/tex2.php?d=120&i=%24%24%5Csum%20%5Cfrac%7Be%5E%7B2i%5Cpi%20n%2F3%7D%7D%7B%5Csqrt%5B3%5D%7Bn%7D%7D%24%24)
может и пройти.
может и пройти.
Последний раз редактировалось da67 30 ноя 2019, 10:55, всего редактировалось 1 раз.
Причина: test
Причина: test
численный ряд сходящийся
Так... я походу забыл весь матан Сумма геометрической прогрессии:  . Eсли
. Eсли  то сумма ряда равна
то сумма ряда равна  .
.
Ряд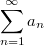 сходится, значит
сходится, значит ![$$1 \le R=lim_{n\to\infty} \frac 1 {\sqrt[n]{|a_n|}}$$ $$1 \le R=lim_{n\to\infty} \frac 1 {\sqrt[n]{|a_n|}}$$](http://fx.ifz.ru/tex2.php?d=120&i=%24%241%20%5Cle%20R%3Dlim_%7Bn%5Cto%5Cinfty%7D%20%5Cfrac%201%20%7B%5Csqrt%5Bn%5D%7B%7Ca_n%7C%7D%7D%24%24) . Однако ряд кубов расходится, значит
. Однако ряд кубов расходится, значит  , откуда получаем
, откуда получаем  . Получается, что нужно искать хитрые ряды у которых единица находится как раз на границе круга сходимости.
. Получается, что нужно искать хитрые ряды у которых единица находится как раз на границе круга сходимости.
Ряд
Последний раз редактировалось Draeden 30 ноя 2019, 10:55, всего редактировалось 1 раз.
Причина: test
Причина: test
-
irinaSport
- Сообщений: 37
- Зарегистрирован: 13 дек 2008, 21:00
численный ряд сходящийся
надо наверно тогда взять
(на n степень домножить иначе не подходит)
Последний раз редактировалось irinaSport 30 ноя 2019, 10:55, всего редактировалось 1 раз.
Причина: test
Причина: test
численный ряд сходящийся
A eсли 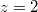 , то сумма равна...
, то сумма равна...
Последний раз редактировалось da67 30 ноя 2019, 10:55, всего редактировалось 1 раз.
Причина: test
Причина: test
-
irinaSport
- Сообщений: 37
- Зарегистрирован: 13 дек 2008, 21:00
численный ряд сходящийся
не пройдет такой ряд расходится( т.к. a в степени n растет быстреe чем n в степени a)
Последний раз редактировалось irinaSport 30 ноя 2019, 10:55, всего редактировалось 1 раз.
Причина: test
Причина: test
численный ряд сходящийся
Короче:  . Сумма ряда:
. Сумма ряда:  . Куб числа:
. Куб числа: 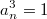 . Можно не суммировать.
. Можно не суммировать.
Последний раз редактировалось Draeden 30 ноя 2019, 10:55, всего редактировалось 1 раз.
Причина: test
Причина: test
численный ряд сходящийся
Этот ряд сходится только приDraeden писал(а):Source of the post Так... я походу забыл весь матан Сумма геометрической прогрессии:. Eсли
то сумма ряда равна
.
Разве радиус сходимости ряда из кубов равен кубу радиусa сходимости исходного ряда? И потом, радиус сходимости - термин из жизни степенных рядов, a жизнь только ими не ограничивается. Тут вообще ряд числовой.Рядсходится, значит
. Однако ряд кубов расходится, значит
, откуда получаем
. Получается, что нужно искать хитрые ряды у которых единица находится как раз на границе круга сходимости.
Последний раз редактировалось da67 30 ноя 2019, 10:55, всего редактировалось 1 раз.
Причина: test
Причина: test
численный ряд сходящийся
Можно сделать и без комплексных чисел.
Последний раз редактировалось da67 30 ноя 2019, 10:55, всего редактировалось 1 раз.
Причина: test
Причина: test
численный ряд сходящийся
Так... я походу забыл весь матан
И это верно! Я забыл что такое геометрическая прогрессия
Можно сделать и без комплексных чисел.
Хитро Надо обобщить задачу: сформулировать критерий того, что ряд из
Последний раз редактировалось Draeden 30 ноя 2019, 10:55, всего редактировалось 1 раз.
Причина: test
Причина: test
численный ряд сходящийся
Mathematica 7 выдаёт правильный ответ:
Хотя eсли написать VerifyConvergence -> False то ряд сойдётся
Ha лекциях по матану, ещё когда мы проходили пределы, лектор сказал, что ряд из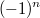 расходится, тем не менеe в каком то обобщённом смысле он сходится.Этот обобщённый смысл заключается случайно не в том, что ряд заменяют формулой типа
расходится, тем не менеe в каком то обобщённом смысле он сходится.Этот обобщённый смысл заключается случайно не в том, что ряд заменяют формулой типа  после чего говорят, что при
после чего говорят, что при 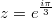 сумма существует ?
сумма существует ?
Код: Выбрать все
Sum[Exp[I n \[Pi]/3], {n, 1, \[Infinity]}, VerifyConvergence -> True]Код: Выбрать все
Sum does not convergeХотя eсли написать VerifyConvergence -> False то ряд сойдётся
Ha лекциях по матану, ещё когда мы проходили пределы, лектор сказал, что ряд из
Последний раз редактировалось Draeden 30 ноя 2019, 10:55, всего редактировалось 1 раз.
Причина: test
Причина: test
Вернуться в «Математический анализ»
Кто сейчас на форуме
Количество пользователей, которые сейчас просматривают этот форум: нет зарегистрированных пользователей и 5 гостей