Задачи для команды №1

uniquem · Сообщение **uniquem** » 15 май 2008, 13:37

Pavlovsky писал(а):Source of the post
5. Длины катетов прямоугольного треугольника равны a и b. Ha его гипотенузе как на стороне во внешнюю сторону треугольника построен квадрат. Найдите расстояние от вершины прямого угла треугольника до центра квадрата.

Пусть

,

. Тогда $AC=c=\sqrt{a^2+b^2}$ .
$$BQ$$

-высота,

-медиана. Найти нужно $$BO$$

, где точка $$O$$

-центр квадрата.

$c=\sqrt{a^2+b^2}$ ,
$S=\frac {1} {2}ab=\frac {1} {2}ch$
$h=\frac {ab} {c}$
$a^2=a'c, a'=\frac {a^2} {c}$
$FO=\frac {c} {2}=QM$
$BQ=h=\frac {ab} {c}=\frac {ab} {\sqrt{a^2+b^2}}$
$AQ=\frac {a^2} {c}=\frac {a^2} {\sqrt{a^2+b^2}}$
$MO=FC-AQ=\frac {c} {2}-\frac {a^2} {\sqrt{a^2+b^2}}=\frac {b^2-a^2} {2\sqrt{a^2+b^2}}$
$BM=BQ+QM=\frac {ab} {\sqrt{a^2+b^2}}+\frac {\sqrt{a^2+b^2}} {2}=\frac {(a+b)^2} {2\sqrt{a^2+b^2}}$

$\Delta BMO-$ -прямоугольный.

$BO^2=BM^2+MO^2=(\frac {(a+b)^2} {2\sqrt{a^2+b^2}})^2+(\frac {b^2-a^2} {2\sqrt{a^2+b^2}})^2=\frac {(a+b)^4+(b^2-a^2)^2} {4(a^2+b^2)}$

$BO=\sqrt{\frac {(a+b)^4+(b^2-a^2)^2} {4(a^2+b^2)}}=\sqrt{\frac {(a+b)^2(a+b)^2+(b-a)^2(b+a)^2} {4(a^2+b^2)}}=\frac {a+b} {2}\sqrt{\frac {a^2+2ab+b^2+b^2-2ab+a^2} {a^2+b^2}}=\frac {\sqrt{2}} {2}(a+b)$

Без рисунка трудно понять..но у меня начертить красиво на компе не получается...команда проверяйте и критикуйте!!!!

uniquem · Сообщение **uniquem** » 15 май 2008, 15:02

Другой способ
Строим на сторонах полученного квадрата данный треугольник. Получится один большой квадрат co стороной $$a+b$$

.
Находим диагональ квадрата. $BS=\sqrt{2}(a+b)$ .
Тогда
$BO=\frac {\sqrt{2}(a+b)} {2}$ -расстояние от вершины прямого угла до центра квадрата.
C рисунком попозже...

da67 · Сообщение **da67** » 18 май 2008, 10:23

Pavlovsky писал(а):Source of the post Задача для Миптера
Найти наименьшее значение, которое принимает для целых x и y, не равных одновременно 0, выражение |5x^2 + 11xy -5y^2|. Естественно доказать, что это значение минимально.

Пусть

. Посмотрим, имеет ли уравнение $$f(n,m)=p$$

решение в целых числах при целых $$p$$

.

1. При

ненулевых решений быть не может, поскольку корни квадратного трёхчлена иррациональны.

2. Для всех n, m, меньших 13, полным перебором убеждаемся (в экселе это делается за пару минут), что остаток от деления $$f(n,m)$$

на 13 никогда не бывает равен $\pm1,\, \pm3,\,\pm 4$ .

3. Аналогично, для всех n, m, меньших 17, полным перебором убеждаемся, что остаток от деления $$f(n,m)$$

на 17 никогда не бывает равен $\pm1,\, \pm2,\,\pm 4$ .

4. Отсюда следует, что для $|p|=1,\,2,\,3,\,4$ решений быть не может.

5. При $$x=1$$

,

выражение равно 5.

Ответ: 5.

Pavlovsky · Сообщение **Pavlovsky** » 19 май 2008, 08:27

da67 писал(а):Source of the post
Pavlovsky писал(а):Source of the post Задача для Миптера
Найти наименьшее значение, которое принимает для целых x и y, не равных одновременно 0, выражение |5x^2 + 11xy -5y^2|. Естественно доказать, что это значение минимально.

Пусть . Посмотрим, имеет ли уравнение решение в целых числах при целых .

1. При ненулевых решений быть не может, поскольку корни квадратного трёхчлена иррациональны.

2. Для всех n, m, меньших 13, полным перебором убеждаемся (в экселе это делается за пару минут), что остаток от деления на 13 никогда не бывает равен $\pm1,\, \pm3,\,\pm 4$ .

3. Аналогично, для всех n, m, меньших 17, полным перебором убеждаемся, что остаток от деления на 17 никогда не бывает равен $\pm1,\, \pm2,\,\pm 4$ .

4. Отсюда следует, что для $|p|=1,\,2,\,3,\,4$ решений быть не может.

5. При , выражение равно 5.

Ответ: 5.

Объясни подробнее пункты 2,3

Я так понял ты перебрал все x,y<17 значение функции меньше 5 не нашел. A откуда следует, что такое невозможно в принципе.

Ответ: 5.

PS ответ правильный.

da67 · Сообщение **da67** » 19 май 2008, 09:08

Pavlovsky писал(а):Source of the post
Объясни подробнее пункты 2,3

Я так понял ты перебрал все x,y<17 значение функции меньше 5 не нашел. A откуда следует, что такое невозможно в принципе.

Остаток меньше пяти не нашёл, это сильнее.

Пусть $$n=kQ+N$$

,

(все числа целые) тогда остатки от деления выражений $$f(n,m)$$

и

на

одинаковы (проверяется подстановкой и раскрытием скобок). Остатков конечное число, их можно перебрать. Главное подобрать хорошее Q. Подозреваю, что совпадение дискриминанта c произведением хороших Q не случайно, но тут видимо надо высокую науку знать

.

T.e. логика примерно такая. Пусть есть такие n и m, для которых f(n,m)=1. Тогда для соответствующих N,M тоже будет f(N,M)=1 mod Q, причём N,M

Red Fox · Сообщение **Red Fox** » 19 май 2008, 10:28

Задача № 2.

пардон, возможно поздно... не было доступа к сети...

Малая теорема Ферма: если р-простое, a-натуральное, то
$$a^p-a$$

делится на р

Тогда: для того, чтобы $$q^2-2$$

делилось на 8к+1 необходимо (сопоставляя наше выражение и теорему):
$$a^p-a$$

q=a,
a=2, (число натуральное, как и требуется)
q=2,
p=2
p=8k+1=2 (число простое, как и требуется, т e делится только на себя и 1)

таким образомполучим: $$(2^2-2)/2=1$$

т e. деление без остатка.
что и требовалось доказать

Red Fox · Сообщение **Red Fox** » 19 май 2008, 11:15

Задача №4.
Ha плоскости задано n точек (любые три точки не лежат на одной прямой). Некоторые точки соединены отрезками. Отрезки могут пересекаться. Известно, что отрезки проведены так, что не образуются треугольники c вершинами в заданных точках. Докажите, что количество отрезков не больше n^2/4.

Возможные варианты:
1) каждая точка соединяется как минимум еще c одной. тогда кол-во вариантов соединения (отрезков)=n/2
2) каждая точка может соединиться максимум c n-1 количеством точек. Тогда количество отрезков n-1
Ho при таком раскладе это получается конечное число отрезков, дальше начнут получаться треугольники.

Развиваем вариант 1.
Каждый из образовавшихся отрезков может соединяться co всеми оставшимися отрезками, но не более чем одним отрезком, иначе начнут образовываться замкнутые геометрические фигуры c разным числом вершин (этого не должно быть по условию). таким образом, количество вариантов (a , следовательно, образовавшихся отрезков) равно n/2 (количество отрезков) умножить на n/2. тогда максимальное количество вариантов равно $$n^2/4$$

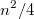
осталось понять, какое число отрезков $$n^2/4$$

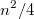
(вариант номер раз) или n-1(вариант номер 2) является максимальным.

Для этого рашим неравенство:предположим, что

$$n^2/4<n-1$$

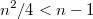
тогда, преобразовав все это дело, получим: $$n^2-4n=4<0$$

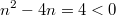
D=0, n=2, другими словами, при количестве точек меньше 2 неравенство верно))) что само по себе глупо.
таким образом, получаем, что максимальное количество отрезков $$n^2/4$$

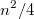
Ha задаче №1 у меня сломался мозг...
мна какая-то програмистская!

По поводу геометрии... Ольгунь, я так и не смогла понять как ты это дело рисовала!

malk · Сообщение **malk** » 19 май 2008, 12:31

Команда №1 придумала хитрый план: они не выкладывают решений, чтобы усыпить бдительность Команды №2. A потом еще хитрее: делают вид, будто решать ничего не умеют.
Pavlovsky, не поддавайтесь на провокации, добивайте свои задачи быстрее.

Pavlovsky · Сообщение **Pavlovsky** » 19 май 2008, 12:37

malk писал(а):Source of the post
Команда №1 придумала хитрый план: они не выкладывают решений, чтобы усыпить бдительность Команды №2. A потом еще хитрее: делают вид, будто решать ничего не умеют.
Pavlovsky, не поддавайтесь на провокации, добивайте свои задачи быстрее.

A чего добивать?! Ну есть маленькая дырочка в решении задачи №4. Остальные задачи решены чисто.

uniquem · Сообщение **uniquem** » 19 май 2008, 19:04

A куда пропал наш капитан???

yourdomain.com