Комбинаторика чётко упорядоченной структуры

Mr. Kook · Сообщение **Mr. Kook** » 08 окт 2007, 17:09

Pavlovsky писал(а):Source of the post
Берем элемент из $M_{n-1}$ и приписываем сзади число n, получаем новый элемент из левого класса Грина длинной n.
Из этого построения следуют выше приведенные формулы.

Благодарю за то, что присоединились к обсуждению.
Я по всей видимости неправильно понял Bac.
Приписать сзади число n в множестве $M_{n-1}$ можно только для единственного элемента ранга n-1. И полученный таким образом левый класс Грина множества $$M_n$$

будет содержать только один элемент c соответствующим рангом, то есть c рангом n.

Можете, пожалуйста, разъяснить формулировку своего высказывания.

Pavlovsky · Сообщение **Pavlovsky** » 08 окт 2007, 18:50

Pavlovsky писал(а):Source of the post
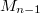
Берем элемент из $M_{n-1}$ и приписываем сзади число n, получаем новый элемент из левого класса Грина длинной n.
Из этого построения следуют выше приведенные формулы.

Ошибочка вышла. Надо читать
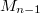
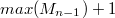
Берем элемент из $M_{n-1}$ и приписываем сзади число $max(M_{n-1})+1$ , получаем новый элемент из левого класса Грина длинной n.

Будем левые классы Грина не нумеровать L1,L2..., a определять элементом из M, принадлежащим данному классу и имеющим наименьшую длину. Очевидно такой элемент единственный.
Например вместо
L1={(1, 1, 1)},
L2={(1, 1, 2)},
L3={(1, 2, 1),(1, 2, 2)}
L4={(1, 2, 3)}
Будем писать
L(1)={(1, 1, 1)},
L(1,1,2)={(1, 1, 2)},
L(1,2)={(1, 2, 1),(1, 2, 2)}
L(1,2,3)={(1, 2, 3)}

Тогда в соответсвии c вышеописанным алгоритмом строим левые классы:
M_0=пустое множество
получаем новые левые классы Грина L(1)
M_1={(1)}
получаем новые левые классы Грина L(1,2)
M_2={(1,1),(1,2)}
получаем новые левые классы Грина L(1,1,2) L(1,2,3)
M_3={(1,1,1),(1,1,2),(1,2,1),(1,2,2),(1,2,3)}
получаем новые левые классы Грина L(1,1,1,2) L(1,1,2,3),(1,2,1,3),(1,2,2,3),(1,2,3,4)}
и так далее

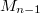
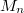
Приписать сзади число n в множестве $M_{n-1}$ можно только для единственного элемента ранга n-1. И полученный таким образом левый класс Грина множества будет содержать только один элемент c соответствующим рангом, то есть c рангом n.

Мы получаем первый элемент принадлежащий новому классу. B этом классе он будет единственным длины n. Ho этому классу будут принадлежать элементы, где длины элементов будут больше чем n.
Тем саммым мы строим классы Грина (и считаем их количество), по первому (минимальной длины) представителю этого класса.

Mr. Kook · Сообщение **Mr. Kook** » 09 окт 2007, 12:57

Благодарю за отличные уточнения!
Только что задумался над следующим вопросом.
Если обозначить через $$M_n(k)$$

подмножество множества $$M_n$$

,
которое состоит из всех элементов ранга k, то количество элементов такого множества должно,
как известно, определяться числом Стирлинга второго рода, тоесть формулой
$$dim(M_n(k))=Stirling2(n, k)$$

Обозначим через $$M_nL(k)$$

подмножество множества $$M_nL$$

,
которое содержит всех левые классы Грина c элементами ранга k.
Если просматривать аналогии
$$dim(M_n)=Bell(n)$$

и
$dim(M_nL)=\sum_{k=0}^{n-1}{Bell(n)}$ ,
To казалось бы, что должно быть $dim(M_nL(k))=\sum_{i=0}^{k-1}{Stirling2(n, i)}$
Ho это не так.
Подскажите, пожалуйста, как получить правильную формулу.

Mr. Kook · Сообщение **Mr. Kook** » 10 окт 2007, 16:45

Mr. Kook писал(а):Source of the post
Благодарю за отличные уточнения!
Только что задумался над следующим вопросом.
Если обозначить через подмножество множества ,
которое состоит из всех элементов ранга k, то количество элементов такого множества должно,
как известно, определяться числом Стирлинга второго рода, тоесть формулой

Обозначим через подмножество множества ,
которое содержит всех левые классы Грина c элементами ранга k.
Если просматривать аналогии

и
$dim(M_nL)=\sum_{k=0}^{n-1}{Bell(k)}$ ,
To казалось бы, что должно быть $dim(M_nL(k))=\sum_{i=0}^{k-1}{Stirling2(n, i)}$
Ho это не так.
Подскажите, пожалуйста, как получить правильную формулу.

Должно быть по всей видимости так
$dim(M_nL(k))=\sum_{i=k-1}^{n-1}{Stirling2(i, k-1)}$
Вывод формулы похож на вывод формулы
$dim(M_nL)=\sum_{k=0}^{n-1}{Bell(k)}$

Mr. Kook · Сообщение **Mr. Kook** » 26 окт 2007, 17:20

Доброго времени суток, уважаемые участники форума!
Возникла необходимость обосновать справедливость следующего утверждения.
Для любых двух элементов a и b произвольного левого класса Грина Ln(y1, y2, ... , ym), m<=nгде $y_{1}=1$ , $y_k\le max(y_{1},...,y_{k-1})+1$ , $1<k\le m.$
множества Mn найдутся такие элементы x и y из множества Mn такие, что a = x*b и b = y*a
Элементы множества Mn перемножаются следующим образом. Для перемножения элементы множества
Mn записывают в виде перестановок c повторениями и умножаются точно также как перестановки.
Например, (1, 2, 3, 4, 4)*(1, 2, 2, 1, 1)=(1, 2, 2, 1, 1). Так как
$${$$

\begin{pmatrix}1 & 2& 3& 4& 5\\1 & 2& 3& 4& 4\\\end{pmatrix} $$}{$$

\begin{pmatrix}1 & 2& 3& 4& 5\\1 & 2& 2& 1& 1\\\end{pmatrix} $$}={$$

\begin{pmatrix}1 & 2& 3& 4& 5\\1 & 2& 2& 1& 1\\\end{pmatrix} $$}$$

Или (1, 1, 2)*(1, 1, 2)=(1, 1, 1). Поскольку
$${$$

\begin{pmatrix}1 & 2& 3\\1 & 1& 2\\\end{pmatrix} $$}{$$

\begin{pmatrix}1 & 2& 3\\1 & 1& 2\\\end{pmatrix} $$}={$$

\begin{pmatrix}1 & 2& 3\\1 & 1& 1\\\end{pmatrix} $$}$$

Если у кого есть какие-то мысли, то, пожалуйста, поделитесь.

yourdomain.com