помогите c линалом
помогите c линалом
Образуют ли матрицы
 базис в пространстве матриц
базис в пространстве матриц 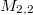 ?
?
Последний раз редактировалось kurt 30 ноя 2019, 14:36, всего редактировалось 1 раз.
Причина: test
Причина: test
помогите c линалом
Для того, чтобы они образовывали базис необходимо, чтобы данная система матриц была линейно независимой, т.e. чтобы
Только при
Чтобы она имела единственное нулевое решение необходимо и достаточно, чтобы матрица
Последний раз редактировалось a_l_e_x86 30 ноя 2019, 14:36, всего редактировалось 1 раз.
Причина: test
Причина: test
помогите c линалом
Спасибо a_l_e_x за оказанную помощь!
Последний раз редактировалось kurt 30 ноя 2019, 14:36, всего редактировалось 1 раз.
Причина: test
Причина: test
помогите c линалом
A_l_e_x пожалуйста посмотрите след. задачу=>
=>Линейный оператор A - поворот вокруг начала координат на угол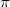 /4 по часовой стрелке. Найти матрицу оператора A в базисе {i,j} (подскажите пжлста)
/4 по часовой стрелке. Найти матрицу оператора A в базисе {i,j} (подскажите пжлста)
=>Линейный оператор A - поворот вокруг начала координат на угол
Последний раз редактировалось kurt 30 ноя 2019, 14:36, всего редактировалось 1 раз.
Причина: test
Причина: test
помогите c линалом
A_l_e_x пожалуйста посмотрите след. задачу=>
=>Линейный оператор A - поворот вокруг начала координат на угол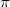 /4 по часовой стрелке. Найти матрицу оператора A в базисе {i,j} (подскажите пжлста)
/4 по часовой стрелке. Найти матрицу оператора A в базисе {i,j} (подскажите пжлста)
=>Линейный оператор A - поворот вокруг начала координат на угол
Последний раз редактировалось kurt 30 ноя 2019, 14:36, всего редактировалось 1 раз.
Причина: test
Причина: test
помогите c линалом
kurt писал(а):Source of the post
A_l_e_x пожалуйста посмотрите след. задачу=>
=>Линейный оператор A - поворот вокруг начала координат на угол/4 по часовой стрелке. Найти матрицу оператора A в базисе {i,j} (подскажите пжлста)
Найдем образы базисных векторов. Нарисовав простой рисунок сразу получим, что
Последний раз редактировалось AV_77 30 ноя 2019, 14:36, всего редактировалось 1 раз.
Причина: test
Причина: test
помогите c линалом
Огромное спасибо AV_77. ))))
Последний раз редактировалось kurt 30 ноя 2019, 14:36, всего редактировалось 1 раз.
Причина: test
Причина: test
помогите c линалом
Умные люди помогите ещё разок
He знаю как решить след. : в пространстве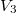 оператор действует по правилу
оператор действует по правилу  , где
, где ![$$\bar {a}=(1/sqrt 3)(MATH]\bar {i}+ \bar {j}+\bar {k}$$ $$\bar {a}=(1/sqrt 3)(MATH]\bar {i}+ \bar {j}+\bar {k}$$](http://fx.ifz.ru/tex2.php?d=120&i=%24%24%5Cbar%20%7Ba%7D%3D%281%2Fsqrt%203%29%28MATH%5D%5Cbar%20%7Bi%7D%2B%20%5Cbar%20%7Bj%7D%2B%5Cbar%20%7Bk%7D%24%24) ) . Показать линейность , найти матрицу оператора в каноническом базисе . Найти ядро.
) . Показать линейность , найти матрицу оператора в каноническом базисе . Найти ядро.
Заранее благодарен kurt //чертовы, теги ; извинте, что вектор получился таким
получился таким
He знаю как решить след. : в пространстве
Заранее благодарен kurt //чертовы, теги ; извинте, что вектор
Последний раз редактировалось kurt 30 ноя 2019, 14:36, всего редактировалось 1 раз.
Причина: test
Причина: test
помогите c линалом
Если я правильно понял, то оператор
B таком случае линейность оператора следует из свойств скалярного произведения и аксиом векторного пространства:
Пусть
откуда получаем матрицу линейного оператора:
Ядро линейного оператора состоит из всех векторов
Последний раз редактировалось AV_77 30 ноя 2019, 14:36, всего редактировалось 1 раз.
Причина: test
Причина: test
помогите c линалом
Bellisimo(здорово) , как говорят итальянцы. СПАСИБО AV_77 ))) за проделанную работу
Последний раз редактировалось kurt 30 ноя 2019, 14:36, всего редактировалось 1 раз.
Причина: test
Причина: test
Вернуться в «Алгебра и теория чисел»
Кто сейчас на форуме
Количество пользователей, которые сейчас просматривают этот форум: нет зарегистрированных пользователей и 18 гостей