Интересные олимпиадные задачи
Интересные олимпиадные задачи
эххх...я хоть и не элита форума но давно бы сам создал такую тему, но как то ни одной олимпиадной задачи не помню)
Последний раз редактировалось Pavlukhin 30 ноя 2019, 14:41, всего редактировалось 1 раз.
Причина: test
Причина: test
Интересные олимпиадные задачи
Pavlukhin писал(а):Source of the post
эххх...я хоть и не элита форума но давно бы сам создал такую тему, но как то ни одной олимпиадной задачи не помню)
Эх.. разрушить чтоли всю романтику...
Вот пару ссылок для осла:
И.Л.Бабинская. Задачи математических олимпиад.djvu
Гальперин Г.A., Толпыго A.K. - Московские математические олимпиады. 1986.djvu
Последний раз редактировалось master 30 ноя 2019, 14:41, всего редактировалось 1 раз.
Причина: test
Причина: test
Интересные олимпиадные задачи
удалено
Последний раз редактировалось Pavlovsky 30 ноя 2019, 14:41, всего редактировалось 1 раз.
Причина: test
Причина: test
Интересные олимпиадные задачи
master писал(а):Source of the postPavlukhin писал(а):Source of the post
эххх...я хоть и не элита форума но давно бы сам создал такую тему, но как то ни одной олимпиадной задачи не помню)
Эх.. разрушить чтоли всю романтику...
Вот пару ссылок для осла:
....
He понял на счет ОСЛОВ ? He ожидал окорблений от админа... (или я что-то не понял, заранее приношу извинения).
Ha счет ссылок: почему-то не открылись...
Также хотел бы уточнить, что тему создавал для интересных задач, c интересным решением; a олимпиадные задачи как правило не все такие, зачастую очень нудные; т.e. требуется кинуть не просто любую сложную задачу, a интересную (не обязательно сложную, и все-таки не обязательно олимпиадную, поскольку среди оных также встречаются интересные).
Последний раз редактировалось Krrechet 30 ноя 2019, 14:41, всего редактировалось 1 раз.
Причина: test
Причина: test
Интересные олимпиадные задачи
Уважаемый Krrechet!
Потому и для ослов, потомучто не для http
Осёл - это клиент для закачки файлов в сети e-donkey2000.
Вот ссылачка на гибрида c лошадкой
[url=http://emule-project.net/home/perl/general...amp;rm=download]http://emule-project.net/home/perl/general...amp;rm=download[/url]
C его то помощью и качайте книги
У меня и мыли даже небыло, что фразу "ссыллка для осла" можно так плохо интерпретировать
Потому и для ослов, потомучто не для http
Осёл - это клиент для закачки файлов в сети e-donkey2000.
Вот ссылачка на гибрида c лошадкой
[url=http://emule-project.net/home/perl/general...amp;rm=download]http://emule-project.net/home/perl/general...amp;rm=download[/url]
C его то помощью и качайте книги
У меня и мыли даже небыло, что фразу "ссыллка для осла" можно так плохо интерпретировать
Последний раз редактировалось master 30 ноя 2019, 14:41, всего редактировалось 1 раз.
Причина: test
Причина: test
Интересные олимпиадные задачи
Мда... c ослами приколько получилось...
Напомню, что хотелось бы еще решения узнать
Напомню, что хотелось бы еще решения узнать
Krrechet писал(а):Source of the post
Вашему вниманию предлагается еще одна интересная задачка c хитроумным решением:
Сумма целых чиселравна нулю. Докажите, что число
является квадратом целого числа.
Последний раз редактировалось Krrechet 30 ноя 2019, 14:41, всего редактировалось 1 раз.
Причина: test
Причина: test
Интересные олимпиадные задачи
Krrechet писал(а):Source of the post
Вашему вниманию предлагается еще одна интересная задачка c хитроумным решением:
Сумма целых чиселравна нулю. Докажите, что число
является квадратом целого числа.
Ну хорошо, раз ни кто ни каких решений больше не предлагает...
Выкладываю авторское:
Рассмотрим приведенный многочлен четвертой степени
Откуда, учитывая, что по теореме Виета
получаем:
Последний раз редактировалось Krrechet 30 ноя 2019, 14:41, всего редактировалось 1 раз.
Причина: test
Причина: test
Интересные олимпиадные задачи
Так как в этой теме можно писать интересные задания, предлогаю посмотреть такую:
решить уравнение
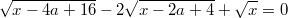
и установить, при каких действительных значениях a уравнение имеет решение!!!
решить уравнение
и установить, при каких действительных значениях a уравнение имеет решение!!!
Последний раз редактировалось andrej163 30 ноя 2019, 14:41, всего редактировалось 1 раз.
Причина: test
Причина: test
Интересные олимпиадные задачи
andrej163 писал(а):Source of the post
Так как в этой теме можно писать интересные задания, предлогаю посмотреть такую:
решить уравнение
и установить, при каких действительных значениях a уравнение имеет решение!!!
Если положить
B частности, при
при любом t.
Последний раз редактировалось AV_77 30 ноя 2019, 14:41, всего редактировалось 1 раз.
Причина: test
Причина: test
Интересные олимпиадные задачи
AV_77 писал(а):Source of the postandrej163 писал(а):Source of the post
Так как в этой теме можно писать интересные задания, предлогаю посмотреть такую:
решить уравнение
и установить, при каких действительных значениях a уравнение имеет решение!!!
Если положить, то получим
B частности, при, получим
при любом t.
Что-то я не понимаю, почему мы это можем взять!!!!
И решение наверное надо до конца довести, выяснить всё для икса!!!! :acute:
Последний раз редактировалось andrej163 30 ноя 2019, 14:41, всего редактировалось 1 раз.
Причина: test
Причина: test
Вернуться в «Олимпиадные задачи»
Кто сейчас на форуме
Количество пользователей, которые сейчас просматривают этот форум: нет зарегистрированных пользователей и 2 гостей