Вот нашёл одну статью - тут вообще целые профессора индуские отжигают.
http://www.ijeter.everscience.org/Manuscripts%5CVolume-3%5CIssue-2%5CVol-3-issue-2-M-10.pdfhttp://www.ijeter.everscience.org/Manuscri...ssue-2-M-10.pdf
У меня конечно лучше получается. Только я похожее решал, но смысл решения одинаковый.
http://www.artofproblemsolving.com/community/c3046h1055253_the_system_of_equations_15http://www.artofproblemsolving.com/communi...of_equations_15
То не знаешь, что решать, то сразу несколько уравняшек появляется.
Посмотрю как эту систему лучше решить - у меня там почему то одно число отрицательным получается.
Формулы для решения Диофантовых уравнений.
-
individ.an
- Сообщений: 760
- Зарегистрирован: 07 фев 2015, 21:00
Формулы для решения Диофантовых уравнений.
Последний раз редактировалось individ.an 27 ноя 2019, 17:47, всего редактировалось 1 раз.
Причина: test
Причина: test
Формулы для решения Диофантовых уравнений.
И действительно. Треш какой-то.individ.an писал(а):Source of the post Вот нашёл одну статью - тут вообще целые профессора индуские отжигают.
В формулировке этих индусов числа могут быть и отрицательными, главное чтоб ненулевыми и различными.individ.an писал(а):Source of the post Посмотрю как эту систему лучше решить - у меня там почему то одно число отрицательным получается.
Нуу, если рассматривать это уравнение как алгебраическое, то оно легко решается. А что позволяет или не позволяет ваш метод - откуда я знаю.individ.an писал(а):Source of the post Для алгебраического уравнения 5-й степени нельзя написать формулу решения, а Вы хотите чтоб я решил более сложное?
Последний раз редактировалось 12d3 27 ноя 2019, 17:47, всего редактировалось 1 раз.
Причина: test
Причина: test
-
individ.an
- Сообщений: 760
- Зарегистрирован: 07 фев 2015, 21:00
Формулы для решения Диофантовых уравнений.
Значит эта системка.

Я сперва нашёл такое решение.
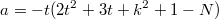
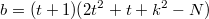
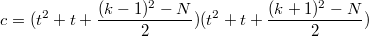
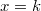
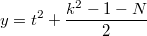
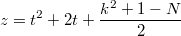
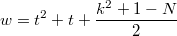
Это мне решение не очень понравилось. И я нашёл такое.
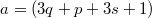









Вот это другое дело. Число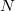 задаётся условием задачи и может быть любым.
задаётся условием задачи и может быть любым.
Я сперва нашёл такое решение.
Это мне решение не очень понравилось. И я нашёл такое.
Вот это другое дело. Число
Последний раз редактировалось individ.an 27 ноя 2019, 17:47, всего редактировалось 1 раз.
Причина: test
Причина: test
Формулы для решения Диофантовых уравнений.
Нет, не другое. И то, и другое, да и сама "система" - идиотизм. Какая тут система, очевидно же, чтоindivid.an писал(а):Source of the post Вот это другое дело.
где
Первое "решение", которое индивид "нашел" - частный случай данного при
Второе "решение" - тут коментар лишний, только можно заметить, что "y" и "N" всегда будут разной четности. А все переменные и константа могут быть одной четности.
Последний раз редактировалось Shadows 27 ноя 2019, 17:47, всего редактировалось 1 раз.
Причина: test
Причина: test
-
individ.an
- Сообщений: 760
- Зарегистрирован: 07 фев 2015, 21:00
Формулы для решения Диофантовых уравнений.
Кретинизм или не кретинизм, но зачем то им эта система нужна была.
Надо будет этим индусам сказать, что они кретины!
Ну да - свести надо к уравнению.
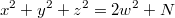
Что я конечно и сделал.
Там просто надо было найти такое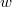 чтоб было больше чем числа
чтоб было больше чем числа 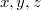
Чтоб наши числа были положительными.
Надо будет этим индусам сказать, что они кретины!
Ну да - свести надо к уравнению.
Что я конечно и сделал.
Там просто надо было найти такое
Чтоб наши числа были положительными.
Последний раз редактировалось individ.an 27 ноя 2019, 17:47, всего редактировалось 1 раз.
Причина: test
Причина: test
-
individ.an
- Сообщений: 760
- Зарегистрирован: 07 фев 2015, 21:00
Формулы для решения Диофантовых уравнений.
Увидел там эту уравняшку.
http://mathoverflow.net/questions/225572/on-cubic-reciprocity-for-x3y3z3-996/225859#225859http://mathoverflow.net/questions/225572/o...6/225859#225859
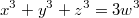
С не совсем умным видом туды завалился и давай формулку рисовать.
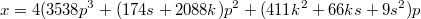
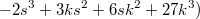
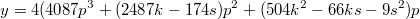
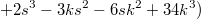
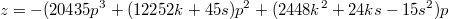
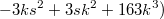
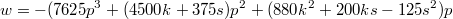
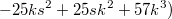
http://mathoverflow.net/questions/225572/on-cubic-reciprocity-for-x3y3z3-996/225859#225859http://mathoverflow.net/questions/225572/o...6/225859#225859
С не совсем умным видом туды завалился и давай формулку рисовать.
Последний раз редактировалось individ.an 27 ноя 2019, 17:47, всего редактировалось 1 раз.
Причина: test
Причина: test
-
individ.an
- Сообщений: 760
- Зарегистрирован: 07 фев 2015, 21:00
Формулы для решения Диофантовых уравнений.
Этот тип меня заколебал. Одно и то же уравнение раз 50 описывает.
Сколько ему формул не рисовал - все не устраивают. Надоел уже.
http://mathoverflow.net/questions/225781/fricke-klein-method-for-isotropic-ternary-quadratic-forms/225995#225995http://mathoverflow.net/questions/225781/f...s/225995#225995
Значит уравнение.
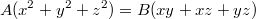
Знаем коэффициент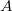 - установим сами число
- установим сами число 
Разложим на множители число.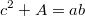
Тогда другой коэффициент будет равен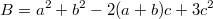
Формулу можно написать сразу.





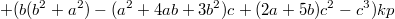


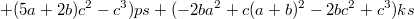
Вот, что можно сделать если использовать три независимых параметров. Как надо искать для нужных нам коэффициентов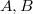 параметры
параметры 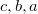 надеюсь объяснять не надо?
надеюсь объяснять не надо?
Сколько ему формул не рисовал - все не устраивают. Надоел уже.
http://mathoverflow.net/questions/225781/fricke-klein-method-for-isotropic-ternary-quadratic-forms/225995#225995http://mathoverflow.net/questions/225781/f...s/225995#225995
Значит уравнение.
Знаем коэффициент
Разложим на множители число.
Тогда другой коэффициент будет равен
Формулу можно написать сразу.
Вот, что можно сделать если использовать три независимых параметров. Как надо искать для нужных нам коэффициентов
Последний раз редактировалось individ.an 27 ноя 2019, 17:47, всего редактировалось 1 раз.
Причина: test
Причина: test
Формулы для решения Диофантовых уравнений.
Я посмотрела там твоё решение. Меня удивил комментарий одного юзера:individ.an писал(а):Source of the post Увидел там эту уравняшку. http://mathoverflow.net/questions/225572/o...6/225859#225859
Не поняла, чего ему не хватает-то? Твои формулы как раз и дают бесконечную серию целочисленных решений. А он пишет, что рациональная параметризация давно известна, а вот решить в целых числах значительно сложнее.Parametrisations of the rational solutions to x^3 +y^3 +z^3 =t are well-known, see for example page 1 of Manin's book on cubic forms. This question is about integer solutions, which is a different problem and much more difficult.
Ну, это я так перевела, а может, он и не то совсем сказал.
Тебя на форуме Math Help Planet тоже забанили что ли?
Во блин!!! Как не в своей стране живём Будем через иностранные форумы сообщения читать своих людей.
Я там тему открыла об этом уравнении, оно меня заинтересовало. Попутно узнала о решении задачи о четырёх кубах, в которой наш Георгий отличился. Вот и Георгий отсюда давно слинял, а на MHP участвует.
Твои формулы проверила для некоторых значений параметров, все решения получились правильные.
Всех там спрашиваю-спрашиваю: есть ли альтернативная формула (для твоей); все молчат, как партизаны.
В общем, ты тему почитай, если писать тебе там нельзя:
http://www.mathhelpplanet.com/viewtopic.php?f=51&t=45672http://www.mathhelpplanet.com/viewtopic.php?f=51&t=45672
P.S. Кстати, спасибо тебе за ссылку на тот иностранный форум. Я там тоже вопросик запостила о магическом тессеракте. Иностранцы вроде ничего, спокойно отнеслись, гнилыми помидорами не стали забрасывать, даже две бронзовые медали выдали сразу
Ну, решить-то задачу они вряд ли решат, по крайней мере, подумают.
http://mathoverflow.net/questions/225907/magic-tesseract-of-order-3-composed-of-prime-numbershttp://mathoverflow.net/questions/225907/m...f-prime-numbers
Последний раз редактировалось omega 27 ноя 2019, 17:47, всего редактировалось 1 раз.
Причина: test
Причина: test
-
individ.an
- Сообщений: 760
- Зарегистрирован: 07 фев 2015, 21:00
Формулы для решения Диофантовых уравнений.
На Матхелпланет меня давно забанили. По просьбе Шведки. Хотя ну её в болото!
Что же касаемо уравнения. Мой один знакомый сайт имеет - там собирает тоджества всякие кто когда найдёт.
https://sites.google.com/site/tpiezas/https://sites.google.com/site/tpiezas/
Если выяснить надо есть ли какие решения там надо посмотреть. Довольно забавные формулки есть.
В большинстве своём народ эти формулы нашёл догадкой или заметил красивую подстановку.
Хотя мои формулы он тоже не очень любит - поэтому их вроде игнорирует.
Можно заметить, что там формулки маленькие, а мои очень громоздкие.
Что же касаемо буржуинового форума. Там будьте крайне осторожны. Если, что разместите в соседних темы.
http://math.stackexchange.com/http://math.stackexchange.com/
http://mathematica.stackexchange.com/http://mathematica.stackexchange.com/
Вообще то там собираются профессиональные математики. И они очень не любят любителей.
Рейтинг по началу могут чуть поднять. Вообще то там с этим беда. Они подымают только своим. Легко можно увидеть как на вообще не за ответ резко подымают одним, а другим понижают.
К тому же профессионалы очень не любят формулы и цифры. Это для них как красная тряпка. Любят очень когда философию человек разводит и стрелочки со знаками и диаграммами рисует.
Попросите решить какое то уравнение - всё! Минусы обеспечены.
Поэтому если надо решить уравнение - лучше этот вопрос на соседних форумах задать. Тем более там просто надо активировать свою учётную запись.
Что меня больше всего раздражает - найдёт кто-то формулку. И все начинают кричать как всё там замечательно и какой он хороший. Хотя часто тривиальшину человек пишет.
А ты там стараешься выводишь сотни формул. И ни чего - все только ругают.
Хотя если просто посмотреть на формулы - просто сравнить их сложность ....
Проблема в этом. Они поддерживают только своих. И если видят в человеке приверженца других идей - начинают бороться с ним.
Что же касаемо уравнения. Мой один знакомый сайт имеет - там собирает тоджества всякие кто когда найдёт.
https://sites.google.com/site/tpiezas/https://sites.google.com/site/tpiezas/
Если выяснить надо есть ли какие решения там надо посмотреть. Довольно забавные формулки есть.
В большинстве своём народ эти формулы нашёл догадкой или заметил красивую подстановку.
Хотя мои формулы он тоже не очень любит - поэтому их вроде игнорирует.
Можно заметить, что там формулки маленькие, а мои очень громоздкие.
Что же касаемо буржуинового форума. Там будьте крайне осторожны. Если, что разместите в соседних темы.
http://math.stackexchange.com/http://math.stackexchange.com/
http://mathematica.stackexchange.com/http://mathematica.stackexchange.com/
Вообще то там собираются профессиональные математики. И они очень не любят любителей.
Рейтинг по началу могут чуть поднять. Вообще то там с этим беда. Они подымают только своим. Легко можно увидеть как на вообще не за ответ резко подымают одним, а другим понижают.
К тому же профессионалы очень не любят формулы и цифры. Это для них как красная тряпка. Любят очень когда философию человек разводит и стрелочки со знаками и диаграммами рисует.
Попросите решить какое то уравнение - всё! Минусы обеспечены.
Поэтому если надо решить уравнение - лучше этот вопрос на соседних форумах задать. Тем более там просто надо активировать свою учётную запись.
Что меня больше всего раздражает - найдёт кто-то формулку. И все начинают кричать как всё там замечательно и какой он хороший. Хотя часто тривиальшину человек пишет.
А ты там стараешься выводишь сотни формул. И ни чего - все только ругают.
Хотя если просто посмотреть на формулы - просто сравнить их сложность ....
Проблема в этом. Они поддерживают только своих. И если видят в человеке приверженца других идей - начинают бороться с ним.
Последний раз редактировалось individ.an 27 ноя 2019, 17:47, всего редактировалось 1 раз.
Причина: test
Причина: test
Формулы для решения Диофантовых уравнений.
Omega, Вы внимательно прочитали пост топикстартера? Человек пишет, что для уравненияomega писал(а):Source of the post Не поняла, чего ему не хватает-то? Твои формулы как раз и дают бесконечную серию целочисленных решений. А он пишет, что рациональная параметризация давно известна, а вот решить в целых числах значительно сложнее.
Иначе уравнение
И Daniel Loughran обясняет индивиду (вот оптимист ), что параметризация данного уравнения в рациональных числах хорошо известна.(И не только для 3 - в правой части, но и для любого рационального t). Но помочь это никак не может.(при каких значений параметров получится W=1???) И индивид, как всегда, в неадеквате.
А если и Вам как индивиду нравятся тупые неполные решения - пожалуйста. Хотя бы имеют человеческий вид:
p,q - взаимнопростые.
Последний раз редактировалось Shadows 27 ноя 2019, 17:47, всего редактировалось 1 раз.
Причина: test
Причина: test
Вернуться в «Алгебра и теория чисел»
Кто сейчас на форуме
Количество пользователей, которые сейчас просматривают этот форум: нет зарегистрированных пользователей и 3 гостей