Эффект Доплера

Анж · Сообщение **Анж** » 13 ноя 2014, 05:58

Не знаю как на счет электромагнитного поля, а магнитное че-то не хочет зеркалом отражаться. Два магнитика отталкиваются, а зеркало и магнитик - никакой реакции.

12d3 · Сообщение **12d3** » 13 ноя 2014, 07:00

Анж писал(а):Source of the post Может быть, обычно исходят из установки "раз и навсегда установленного центра массы"?

Нет такой установки. Анж, давайте я честно интегрированием все посчитаю. Если вы не против, то я начну.
Сначала вспомогательная задача номер 1. Есть тонкое кольцо радиуса R и массой m. Найти напряженность поля в точке на оси кольца на расстоянии h от центра кольца.
Возьмем элемент кольца массой $$dm$$

. Расстояние от точки до этого элемента равно $\sqrt{h^2+R^2}$ . Соответственно напряженность, создаваемая этим элементом равна $\frac{Gdm}{h^2+R^2}$ . Напряженность - это вектор, и поэтому мы должны векторно просуммировать напряженности от всех элементов. Поскольку у нас картинка симметрична относительно вертикальной оси, то результирующая напряженность будет направлена вдоль этой оси. Значит, нам нужно просуммировать проекции напряженностей от каждого элемента на вертикальную ось. Проекция от одного элемента равна $\frac{Gdm}{h^2+R^2} \cdot \frac{h}{\sqrt{h^2+R^2}} = \frac{Ghdm}{\left ( h^2+R^2 \right )^{\frac{3}{2}}}$ . Значит суммарная напряженность равна $\int \frac{Ghdm}{\left ( h^2+R^2 \right )^{\frac{3}{2}}} = \frac{Ghm}{\left ( h^2+R^2 \right )^{\frac{3}{2}}}$ .
Если есть вопросы и возражения, спрашивайте.

12d3 · Сообщение **12d3** » 13 ноя 2014, 07:18

Вспомогательная задача номер 2. Кольцо теперь толстое, с внутренним радиусом r, внешним радиусом R, массой M. Так же нужно найти напряженность поля в точке на оси кольца на расстоянии h от центра кольца.
Разобьем наше толстое кольцо на бесконечно большое количество тонких колец. Толщина тонких колец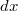 $$dx$$

, радиусы тонких колец изменяются в пределах от $$r$$

до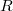

. Площадь толстого кольца $S=\pi \left ( R^2-r^2 \right )$ . Поверхностная плотность $\rho = \frac{M}{S} = \frac{M}{\pi \left ( R^2 - r^2 \right )}$ . Площадь поверхности тонкого кольца $dS = 2\pi x dx$ , соответственно его масса равна $dm = \rho dS = 2\pi \rho x dx$ . Теперь используем результат предыдущей задачи. Напряженность, создаваемая одним кольцом, равна $\frac{Ghdm}{\left ( h^2+x^2 \right )^{\frac{3}{2}}} = \frac{Gh2\pi\rho xdx}{\left ( h^2+x^2 \right )^{\frac{3}{2}}}$ . Теперь, чтоб найти суммарную напряженность, нужно проинтегрировать по всем тонким кольцам.
$\int_{r}^{R} \frac{Gh2\pi\rho xdx}{\left ( h^2+x^2 \right )^{\frac{3}{2}}} = \left. - \frac{Gh2\pi\rho}{\sqrt{ h^2+x^2 }}\right|_r^R = 2\pi \rho Gh \left ( \frac{1}{\sqrt{h^2+r^2}} - \frac{1}{\sqrt{h^2+R^2}} \right ) = \frac{2MGh}{R^2-r^2} \left ( \frac{1}{\sqrt{h^2+r^2}} - \frac{1}{\sqrt{h^2+R^2}} \right )$

Анж · Сообщение **Анж** » 13 ноя 2014, 08:47

12d3 писал(а):Source of the post Сначала вспомогательная задача номер 1.

А вы уверенны, что здесь складывать нужно? По сути, вы привели всю конструкцию к виду: шар с массой m на расстоянии $\sqrt{h^{2}+R^{2}}$ создает ускорение g. Чем меньше h, тем больше g. Но в кольце (а не на шаре), чем меньше h, тем больше они друг другу мешать будут.
Я бы, скорее, от обратного пошла. Пусть шар с массой m на нашем расстоянии, допустим, имеет g= 20, но у нас кольцо, и центр массы "размазан" на 360 градусов. Значит каждый из фрагментов в 1 градус будет создавать в нашей точке g=20/360=0.0555. И не больше. А если по пол градуса, то и меньше. И боюсь, без синусов с косинусами не обойтись.

12d3 · Сообщение **12d3** » 13 ноя 2014, 08:54

Теперь наша исходная задача. Посчитать силу притяжения от Земли с трубой. Пусть радиус земли R, плотность Земли 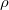$\rho$ , тогда масса Земли без трубы равна $M=\rho \frac{4}{3}\pi R^3$ . Радиус трубы равен r. Посчитаем напряженность поля на расстоянии h от центра Земли.
Разобем нашу Землю на бесконечное количество толстых колец. Толщина колец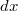 $$dx$$

, где

- это координата центра кольца относительно центра Земли, начало координат в центре Земли. Внутренний радиус кольца всегда равен r, а вот внешний зависит от координаты и равен $\sqrt{R^2 - x^2}$ . Площадь поверхности кольца $S = \pi \left ( \left(\sqrt{R^2 -x^2}\right)^2 - r^2 \right ) = \pi\left ( R^2-r^2 -x^2 \right )$ . Масса кольца $dM = \rho Sdx = \pi \rho \left( R^2-r^2 -x^2 \right )dx$ . Расстояние от точки наблюдения до центра кольца равно $$h-x$$

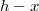Используя результат предыдущей задачи, получим силу притяжения от одного кольца $\frac{2G(h-x)dM}{R^2-r^2-x^2}\left ( \frac{1}{\sqrt{(h-x)^2+r^2}} - \frac{1}{\sqrt{(h-x)^2+(R^2-x^2)}}\right ) = \frac{2G(h-x)\pi\rho (R^2-r^2-x^2)dx}{R^2-r^2-x^2}\left ( \frac{1}{\sqrt{(h-x)^2+r^2}} - \frac{1}{\sqrt{h^2+R^2-2hx}}\right ) =2G(h-x)\pi\rho dx\left ( \frac{1}{\sqrt{(h-x)^2+r^2}} - \frac{1}{\sqrt{h^2+R^2-2hx}}\right )$
Найдем теперь пределы интегрирования. Максимальная и минимальная координата x - это когда внешний радиус кольца становится равен внутреннему. Значит $x_{min} = -\sqrt{R^2-r^2},\,\,\,x_{max} = \sqrt{R^2-r^2}$
Теперь интегрируем. Суммарная напряженность равна $\int_{x_{min}}^{x_{max}}2G(h-x)\pi\rho dx\left ( \frac{1}{\sqrt{(h-x)^2+r^2}} - \frac{1}{\sqrt{h^2+R^2-2hx}}\right ) = \left.2\pi \rho G \left ( -\sqrt{(h-x)^2+r^2} +\sqrt{h^2+R^2-2hx} - \frac{\sqrt{h^2+R^2-2hx}\left ( hx+h^2+R^2 \right )}{3h^2}\right )\right|_{x_{min}}^{x_{max}}=$ Тут три слагаемых, найдем каждое по отдельности.
Первое: $\left. -\sqrt{(h-x)^2+r^2}\right|_{x_{min}}^{x_{max}}=-\sqrt{h^2+r^2+R^2-r^2-2h\sqrt{R^2-r^2}} +\sqrt{h^2+r^2+R^2-r^2+2h\sqrt{R^2-r^2}} = \sqrt{h^2+R^2+2h\sqrt{R^2-r^2}} - \sqrt{h^2+R^2-2h\sqrt{R^2-r^2}}$
Второе: $\left. \sqrt{h^2+R^2-2hx}\right|_{x_{min}}^{x_{max}}=\sqrt{h^2+R^2-2h\sqrt{R^2-r^2}} - \sqrt{h^2+R^2+2h\sqrt{R^2-r^2}}$
Видим, что эти два слагаемых взаимоуничтожаются. Значит, остается только третье:
$\left.-\frac{\sqrt{h^2+R^2-2hx}\left ( hx+h^2+R^2 \right )}{3h^2}\right|_{x_{min}}^{x_{max}} = \frac{1}{3h^2}\left ( -\sqrt{h^2+R^2-2h\sqrt{R^2-r^2}}\left ( h\sqrt{R^2-r^2}+h^2+R^2 \right ) + \sqrt{h^2+R^2+2h\sqrt{R^2-r^2}}\left ( -h\sqrt{R^2-r^2}+h^2+R^2 \right )\right )=$
Итого, суммарная напряженность равна $\frac{2\pi\rho G}{3h^2}\left ( -\sqrt{h^2+R^2-2h\sqrt{R^2-r^2}}\left ( h\sqrt{R^2-r^2}+h^2+R^2 \right ) + \sqrt{h^2+R^2+2h\sqrt{R^2-r^2}}\left ( -h\sqrt{R^2-r^2}+h^2+R^2 \right )\right )$
Громоздко, не правда ли. Наверное, можно упростить, пока не знаю как.

12d3 · Сообщение **12d3** » 13 ноя 2014, 08:55

Анж писал(а):Source of the post И боюсь, без синусов с косинусами не обойтись.

У меня там есть $\frac{h}{\sqrt{h^2+R^2}}$ . Это самый что ни на есть косинус.

12d3 · Сообщение **12d3** » 13 ноя 2014, 09:11

12d3 писал(а):Source of the post Итого, суммарная напряженность равна \frac{2\pi\rho G}{3h^2}\left ( -\sqrt{h^2+R^2-2h\sqrt{R^2-r^2}}\left ( h\sqrt{R^2-r^2}+h^2+R^2 \right ) + \sqrt{h^2+R^2+2h\sqrt{R^2-r^2}}\left ( -h\sqrt{R^2-r^2}+h^2+R^2 \right )\right )

Проверим результат. В случае отсутствия трубы, то есть $$r=0$$

, получим
$\frac{2\pi\rho G}{3h^2}\left ( -\sqrt{h^2+R^2-2hR}\left ( hR+h^2+R^2 \right ) + \sqrt{h^2+R^2+2hR}\left ( -hR+h^2+R^2 \right )\right ) = \frac{2\pi\rho G}{3h^2}\left ( -\left |R-h \right |\left ( hR+h^2+R^2 \right ) + \left |R+h \right |\left ( -hR+h^2+R^2 \right )\right ) = \frac{2\pi\rho G}{3h^2}\left ( \left ( h^2+R^2 \right )\left ( \left | R+h \right | - \left | R-h \right | \right ) -hR \left ( \left | R+h \right | + \left | R-h \right | \right )\right )$
В случае, когда тело над поверхностью, $$h>R$$

, тогда будет $\frac{2\pi\rho G}{3h^2}\left ( \left ( h^2+R^2 \right )\left ( R+h+R-h \right ) -hR \left ( R+h-R+h \right )\right ) = \frac{2\pi\rho G}{3h^2}\left ( (h^2+R^2)2R - hR2h \right ) = \frac{2\pi\rho G}{3h^2}\left ( 2R^3 \right ) = \frac{4\pi R^3}{3}\frac{\rho G}{h^2} = \frac{\rho V G}{h^2} = \frac{MG}{h^2}$ . Квадратичное убывание. Как и должно быть.
В случае, когда тело под поверхностью, $$h<R$$

, тогда будет $\frac{2\pi\rho G}{3h^2}\left ( \left ( h^2+R^2 \right )\left ( R+h-R+h \right ) -hR \left ( R+h+R-h \right )\right ) = \frac{2\pi\rho G}{3h^2}\left ( (h^2+R^2)2h - hR2R \right ) = \frac{2\pi\rho G}{3h^2}\left ( 2h^3 \right ) = \frac{4\pi \rho h G}{3}$
Линейное возрастание. Как и должно быть.
Пока что все сходится.

Анж · Сообщение **Анж** » 13 ноя 2014, 10:18

12d3 писал(а):Source of the post Пока что все сходится.

Только немножко с опытом расходиться. Вам придется убедить тело, что масса из "верхних" слоев на него не действует. А крутильные весы Кавендиша - фикция. Потому, что вся напряженность направлена у нас к центру Земли, а его шары где-то сбоку, и роли играть не могут.

12d3 · Сообщение **12d3** » 13 ноя 2014, 10:28

Анж писал(а):Source of the post Только немножко с опытом расходиться.

С каким опытом? Кто-проводил опыт по бурению Земли насквозь?

Анж писал(а):Source of the post Вам придется убедить тело, что масса из "верхних" слоев на него не действует.

Зачем кого-то убеждать. Действуют все слои, и внешние, и внутренние, и какие угодно. Я убеждаю не тело, а вас.)

ковип · Сообщение **ковип** » 13 ноя 2014, 12:38

Анж писал(а):Source of the post Вы же не знаете, что такое фотон, может он, как раз, как я по отношению к речке, а не как шарик.

Кое что знаю. Во всяком случае столько, что бы не проверять его свойства, на свойствах сахарного песка. Он не может быть как вы, у него нет массы покоя. Вследствие чего, он чем быстрее колеблется, тем тяжелее.
Это как в том анекдоте. Мать заорала на детей"ложитесь спать!!!" так, что все соседи полезли в постель. Мало ли что.
А если (орать) колебаться перестанет, его не станет. Знаете в чём суть интерференции? Колебания противоположные по фазе вычитаются. Представляете какая дикость? Летят два фотона сталкиваются и исчезают БЕССЛЕДНО. А некоторые сталкиваются и не только не исчезают но, и ещё другие фотоны создают. Интерференция, мать её! Это она полосочки на экране "рисует", когда существует разница фаз двух ЭМ волн.

yourdomain.com