Анику про механику

Рубен · Сообщение **Рубен** » 22 фев 2014, 10:48

Anik писал(а):Source of the post По поводу минуса в правой части я ещё не уверен, но буду иметь в виду. Война план покажет.

а без войны никак? Вы просто неверно записали силу упругости - она направлена против радиус-вектора, а у вас по нему.

Anik · Сообщение **Anik** » 22 фев 2014, 11:31

Рубен писал(а):Source of the post
Anik писал(а):Source of the post По поводу минуса в правой части я ещё не уверен, но буду иметь в виду. Война план покажет.
а без войны никак? Вы просто неверно записали силу упругости - она направлена против радиус-вектора, а у вас по нему.

"Война показала", что вы правы. Поставлю-ка я там минус.
Спасибо!

Рубен · Сообщение **Рубен** » 22 фев 2014, 12:11

Для полярного радиуса $$r$$

любого шарика получается такое уравнение:

$\displaystyle \ddot r r^3 + \Omega^2 r^4 = A, \;\; A = \omega_0^2 r^4_0, \;\; \Omega^2 = k\frac {m_1+m_2}{m_1m_2}.$

$\displaystyle \omega_0, r_0$ - начальные угловая скорость и положение шарика.

Переменные разделяются и уравнение решается в квадратурах, но вот берется ли интеграл?

Anik · Сообщение **Anik** » 22 фев 2014, 13:06

$\displaystyle \begin{cases} 2\dot R_1\dot\varphi+R_1\ddot\varphi=0 \\ m_1\ddot R_1-m_1R_1\dot\varphi^2=-\frac{k(m_1+m_2)}{m_2}R_1 \end{cases}$
Решение этой системы уравнений мы попробуем угадать, исходя из механических соображений.
В качестве одного из возможных видов движения, предположим равномерное движение по окружности с постоянным радиусом $$R_1$$

.
Из первого уравнения сразу следует, что $\dot R_1= 0$ и $\ddot\varphi=0$ и уравнение обращается в тождество 0=0.
Из второго уравнения получаем:
$\dot\varphi^2=\frac{k(m_1+m_2)}{m_1m_2}$ или:
$\dot\varphi=\sqrt{\frac{k(m_1+m_2)}{m_1m_2}}$
Теперь, воспользуемся тем, что вес точки $$m_1$$

при равномерном вращении уравновешивается силой натяжения пружины $$k_1R_1$$

. Вес точки: $P=m_1R_1\dot\varphi^2$ . Имеем:
$m_1R_1\dot\varphi^2=k_1R_1$ . Отcюда находим $k_1=m_1\dot\varphi^2\qquad (*)$
Второе дифференциальное уравнение, с учётом того, что $$R_1-const$$

перепишем так
$m_1R_1\dot\varphi^2=k_1R_1$
Подставляя сюда найденное значение $$k_1$$

из (*), видим, что второе уравнение тоже обращается в тождество, следовательно, найденное решение удовлетворяет двум дифференциальным уравнениям.

Рубен · Сообщение **Рубен** » 22 фев 2014, 14:17

Anik писал(а):Source of the post Решение этой системы уравнений мы попробуем угадать

Да, такое бывает.

, исходя из механических соображений.

А вот это пурга. Нет никаких "механических соображений".

В качестве одного из возможных видов движения, предположим равномерное движение по окружности с постоянным радиусом

Да, такое движение является решением уравнения, но только при очень специальный начальных условиях. При этих начальных условиях ответ можно было сказать сразу вообще не составляя никаких уравнений:

$R=\mathrm {const},\;\;\;\omega = \sqrt{\frac {k} {m}};$

$\displaystyle m = \frac {m_1m_2} {m_1+m_2}.$

Это хорошо известное тривиальное решение. Однако, предполагается, что начальные условия произвольные.

Напомню:

grigoriy писал(а):Source of the post Аник, шоб шарики с пружинкой не только вращались, но и пульсировали. Заметано?

Anik · Сообщение **Anik** » 22 фев 2014, 14:28

Рубен писал(а):Source of the post
Это хорошо известное тривиальное решение. Однако, предполагается, что начальные условия произвольные.

Напомню:
grigoriy писал(а):Source of the post Аник, шоб шарики с пружинкой не только вращались, но и пульсировали. Заметано?

~~Там в последней формуле опечатка.~~ ***
Да я понимаю, но не всё сразу!

Anik · Сообщение **Anik** » 22 фев 2014, 15:38

Нужно провести ещё анализ полученного решения и сделать выводы.
Как следует из формулы:
$\dot\varphi=\sqrt{\frac{k(m_1+m_2)}{m_1m_2}}$ ,
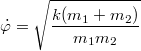Угловая скорость вращения не зависит от заданного начального кинетического момента. Следовательно, она не зависит и от энергии системы. Вообще это замечательный факт!
Теперь, найдём потенциальную и кинетическую энергии системы, при равномерном вращении.
Для пружины:
$$A_{ïð}=1/2k_1R_1$$
Кинетическая энергия вращающегося шарика:
$T=1/2J\dot\varphi^2=1/2m_1R_1^2\dot\varphi^2$
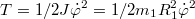
***Учитывая, что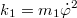 $k_1=m_1\dot\varphi^2$ , как мы нашли раньше, получим:
$$A_{ïð}=T$$
Т.е. потенциальная энергия растянутой пружины равна равна кинетической энергии вращения, при вращении с постоянной скоростью.
Это второй замечательный факт. Эти факты замечательны, несмотря на то, что они общеизвестны.
***Как бы сильно пружина ни была растянута (при различных кинетических моментах), её период обращения один и тот же.

Рубен · Сообщение **Рубен** » 22 фев 2014, 15:53

Anik писал(а):Source of the post Угловая скорость вращения не зависит от заданного начального кинетического момента. Следовательно, она не зависит и от энергии системы. Вообще это замечательный факт!

Так это и так понятно, что если нет колебаний (вы ведь сами постулировали, что R = const), то и кинетическая энергия сохраняется и угловая скорость. А что тут удивительного? За счет чего будет меняться угловая скорость, если момент инерции постоянный? Но это ведь не общее решение, а только один тривиальный случай.

Рубен · Сообщение **Рубен** » 22 фев 2014, 16:04

Рубен писал(а):Source of the post
Для полярного радиуса любого шарика получается такое уравнение:

$\displaystyle \ddot r r^3 + \Omega^2 r^4 = A, \;\; A = \omega_0^2 r^4_0, \;\; \Omega^2 = k\frac {m_1+m_2}{m_1m_2}.$

$\displaystyle \omega_0, r_0$ - начальные угловая скорость и положение шарика.

Переменные разделяются и уравнение решается в квадратурах, но вот берется ли интеграл?

Интеграл берется. Общее решение, если не накосячил, будет таким:

$$\displaystyle \mathrm{r}(t) = \sqrt{\frac {c_1} {\Omega}\left[ 1 + \sqrt {1 - \left ( \frac {\omega_0 \mathrm{r_0}^2} {ñ_1}\right)^2}\cdot \sin(2\Omega t +c_2) \right]} $$</span> <span class=

$$" title="$$ $$" align="middle" style="border: 0; vertical-align: middle">\displaystyle \varphi (t) = \left[ \omega_0 \left (\frac {\mathrm{r_0}} {\mathrm{r(t)}}\right)^2 \right]\cdot t $$</span> <span class=

$$" title="$$ $$" align="middle" style="border: 0; vertical-align: middle">c_1,c_2$$ - постоянные, определяемые из Н.У., но искать мне их неохота.

Anik · Сообщение **Anik** » 22 фев 2014, 16:34

Рубен писал(а):Source of the post
А что тут удивительного? За счет чего будет меняться угловая скорость, если момент инерции постоянный?

Удивительное в том, что при любом начальном кинетическом моменте угловая скорость вращения будет одна и та же. При увеличении начального кинетического момента увеличивается длина пружины и линейная скорость точек, а вот угловая скорость постоянна, она определяется только жёсткостью пружины и массами точек, которые не меняются.
Это похоже на то, что частота (и период) собственных колебаний не зависит от амплитуды, а определяется только жёсткостью пружины и колеблющейся массой.

yourdomain.com