Задачка для любителей неравенств и не только
- JeffLebovski
- Сообщений: 650
- Зарегистрирован: 06 апр 2011, 21:00
Задачка для любителей неравенств и не только
Пусть 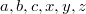 - положительные числа, такие что
- положительные числа, такие что  . Докажите, что
. Докажите, что 
Последний раз редактировалось JeffLebovski 28 ноя 2019, 15:51, всего редактировалось 1 раз.
Причина: test
Причина: test
Задачка для любителей неравенств и не только
Сразу показалось подозрительным такое обилие свободных параметров(но руки дошли только через 2 недели). Контрпример 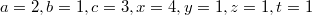
Последний раз редактировалось Ian 28 ноя 2019, 15:51, всего редактировалось 1 раз.
Причина: test
Причина: test
- JeffLebovski
- Сообщений: 650
- Зарегистрирован: 06 апр 2011, 21:00
Задачка для любителей неравенств и не только
Последний раз редактировалось JeffLebovski 28 ноя 2019, 15:51, всего редактировалось 1 раз.
Причина: test
Причина: test
Задачка для любителей неравенств и не только
Ну ладно. При t=0 и t=-1 неравенство обращается в тождественное равенство. И что же , производные левой и правой частей по t в этих точках тождественно равны?
Последний раз редактировалось Ian 28 ноя 2019, 15:51, всего редактировалось 1 раз.
Причина: test
Причина: test
- JeffLebovski
- Сообщений: 650
- Зарегистрирован: 06 апр 2011, 21:00
Задачка для любителей неравенств и не только
Последний раз редактировалось JeffLebovski 28 ноя 2019, 15:51, всего редактировалось 1 раз.
Причина: test
Причина: test
Вернуться в «Олимпиадные задачи»
Кто сейчас на форуме
Количество пользователей, которые сейчас просматривают этот форум: нет зарегистрированных пользователей и 2 гостей