Задача эффективно двумерная. В области
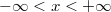
,
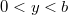
вода течет в положительном направлении оси

, в области
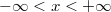
,
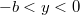
--- в отрицательном. На границах {
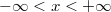
,
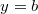
}, {
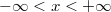
,
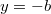
}, {
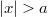
,
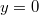
} обращается в нуль тепловой поток, а в окне {
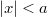
,
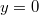
} непрерывны температура и тепловой поток. Без ограничения общности можно считать, что на входе в теплообменник, то есть при {
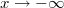
,
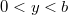
} и при {
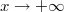
,
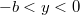
} температура равна +1 и -1 соответственно. Нужно определить температуру на выходе, то есть при {
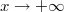
,
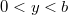
} и при {
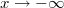
,
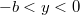
}.
Заглядываем в ЛЛ6, параграф "Теплопроводность в несжимаемой жидкости" и пишем уравнение (50,1), считая все коэффициенты постоянными, а скорость не зависящей от координат

В нашем случае уравнения при
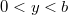
и
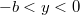
будут

Обезразмерим задачу. Введем безразмерные параметры
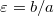
,
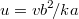
, и безразмерные координаты
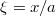
,
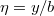
. Тогда



Значения на входе в теплообменник

Нетрудно догадаться, что аналогия с поездами будет достигаться, когда параметр

мал. Параметр же
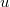
можно считать как конечным, так и малым вместе с

.
Решение удобно представить через функцию Грина. Введем оператор

и сопряженный к нему оператор

Тогда
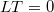
, а уравнение для функции Грина

Граничные условия

. На обеих бесконечностях

при
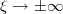
. А вот сама функция Грина не может стремиться к нулю сразу на обеих бесконечностях. Это очевидно, если проинтегрировать уравнение для нее по полосе
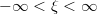
,
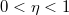

В качестве условия на бесконечности удобно задать
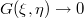
при
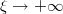
. Тогда
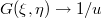
при
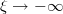
. Пишем



При

имеем

Последняя полученная нами формула довольно очевидна из "пальцевых" соображений: интеграл справа представляет собой полный поток тепла через окно, а множитель
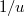
--- время прохода данной порции воды вдоль окна.
Чтобы найти тепловой поток
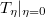
через окно
, воспользуемся симметрией температуры. Пишем


и складываем эти равенства
![$$\displaystyle 2=\int_{-1}^1d\xi\,T_\eta(\xi,0)[G(\xi,0;\xi',0)+G(-\xi,0;-\xi',0)]. $$ $$\displaystyle 2=\int_{-1}^1d\xi\,T_\eta(\xi,0)[G(\xi,0;\xi',0)+G(-\xi,0;-\xi',0)]. $$](http://fx.ifz.ru/tex2.php?d=120&i=%24%24%5Cdisplaystyle%20%202%3D%5Cint_%7B-1%7D%5E1d%5Cxi%5C%2CT_%5Ceta%28%5Cxi%2C0%29%5BG%28%5Cxi%2C0%3B%5Cxi%26%2339%3B%2C0%29%2BG%28-%5Cxi%2C0%3B-%5Cxi%26%2339%3B%2C0%29%5D.%20%24%24)
Поскольку функция Грина зависит в действительности только от

, в квадратных скобках стоит четная функция

. Мы получили интегральное уравнение относительно
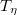
. Для фактического его решения нужно определить функцию Грина.
Будем искать ее в виде разложения по собственным функциям оператора
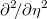
с граничными условиями


Коэффициенты удовлетворяют уравнениям

Решения соответствующих однородных уравнений, производные которых убывают при
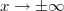
, равны соответственно
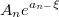
и
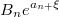
, где

--- корни уравнения
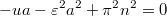
. Коэффициенты
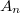
,
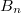
определяются из условий непрерывности коэффициентов
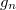
при

и скачка их производных
![$$-\varepsilon^2[g'_n(\xi'+0)-g'_n(\xi'-0)]=2\cos\pi n\eta'$$ $$-\varepsilon^2[g'_n(\xi'+0)-g'_n(\xi'-0)]=2\cos\pi n\eta'$$](http://fx.ifz.ru/tex2.php?d=120&i=%24%24-%5Cvarepsilon%5E2%5Bg%26%2339%3B_n%28%5Cxi%26%2339%3B%2B0%29-g%26%2339%3B_n%28%5Cxi%26%2339%3B-0%29%5D%3D2%5Ccos%5Cpi%20n%5Ceta%26%2339%3B%24%24)
. Окончательно

Ядро интегрального уравнение для
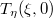
имеет вид


Отметим, что интеграл от убывающих на бесконечности членов равен


Полного решения этого интегрального уравнения у меня на данный момент нет, но есть простая оценка, правда, основанная на недоказанном, но весьма естественном предположении, что всюду в окне
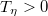
.
Обозначим полный тепловой поток сквозь окно через

Интегрируя уравнение
![$$\displaystyle 2=\int_{-1}^1d\xi\,T_\eta(\xi,0)[1/u+\tilde K(\xi-\xi')] $$ $$\displaystyle 2=\int_{-1}^1d\xi\,T_\eta(\xi,0)[1/u+\tilde K(\xi-\xi')] $$](http://fx.ifz.ru/tex2.php?d=120&i=%24%24%5Cdisplaystyle%20%202%3D%5Cint_%7B-1%7D%5E1d%5Cxi%5C%2CT_%5Ceta%28%5Cxi%2C0%29%5B1%2Fu%2B%5Ctilde%20K%28%5Cxi-%5Cxi%26%2339%3B%29%5D%20%24%24)
по

, получаем

откуда

и

Минимальное значение
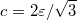
достигается при
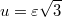
и приводит к наилучшей оценке для
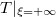
.
P. S. Оценка выходной температуры с обратной стороны совершенно очевидная, даже забыл сразу написать. Имеем

откуда
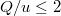
и

Разумеется, эта оценка очевидна и из более общих соображений: в противном случае можно было бы использовать теплообменник как вечный двигатель второго рода.