Доказать, что не существует

Sonic86 · Сообщение **Sonic86** » 26 июл 2011, 11:48

Рассуждения в методе спуска удобно проводить полностью.
Странное у Вас какое-то уравнение. Вы уверены, что оно спуском решается? По-моему нет: в сумму 3-х квадратов не разлагаются лишь числа вида $$8k-7$$

, правая часть уже не такая.

Вот Вам пример: $$x^2+y^2 = 3(u^2+v^2)$$

. Или еще лучше: $$x^2 = 2y^2$$

. Проводите рассуждения полностью: пусть есть решение. Тогда делаем то-то и получаем новое решение, компоненты которого по модулю меньше компонент предыдущего решения. Это противоречит конечности множества натуральных чисел снизу. Значит ля-ля-ля.

Clever_Unior

В первом примере так:
$$x^2+y^2=9(x_1^2+y_1^2)$$

?
Отсюда все делится на 3, да?

Sonic86 · Сообщение **Sonic86** » 26 июл 2011, 14:32

Clever_Unior писал(а):Source of the post
В первом примере так:

?
Отсюда все делится на 3, да?

Непонятно, откуда 1-е равенство (его не должно быть вообще). В целом, очень отрывочно, без начала и конца. Т.е., пишите полностью и подробно - Вам же понятнее станет.

Clever_Unior

Clever_Unior писал(а):Source of the post
В первом примере так:

?
Отсюда все делится на 3, да?

Так как:

Левая часть тоже должна делится на 3. Так как в квадрате числа дают при делении на 3 остаток или 0 или 1, то и х и у кратны трем. Отсюда запишем:
$$x^2+y^2=9(x_1^2+y_1^2)$$

Тогда:

Аналогично сокращаем...

Sonic86 · Сообщение **Sonic86** » 26 июл 2011, 19:08

Clever_Unior писал(а):Source of the post
Так как:

Левая часть тоже должна делится на 3. Так как в квадрате числа дают при делении на 3 остаток или 0 или 1, то и х и у кратны трем. Отсюда запишем:

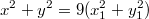
Тогда:

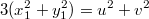
Аналогично сокращаем...

А, понял (туплю просто). Вы ввели $$x=3x_1, y=3y_1$$

, но этого не написали. И зря! Эти соотношения - основные для обоснования метода бесконечного спуска. Наконец, Вы не написали, что происходит после того, как мы аналогично сокращаем. Еще раз скажу: что там будет - понятно, но Вам надо подробно это написать, чтобы вам же стало понятнее и запомнилось лучше.

Показываю на примере: $$x^2=2y^2$$

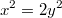
. Докажем, что это уравнение имеет лишь одно решение $$(0;0)$$

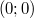
. Предположим, противное, что существует натуральное решение $$(x,y)$$

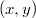
такое, что $x \neq 0$ , тогда и $x,y \geqslant 1$ . $x^2=2y^2 \Rightarrow 2|x^2 \Rightarrow 2|x \Leftrightarrow x=2x_1$ . Подставляем:
$x^2=2y^2 \Rightarrow 2|x^2 \Rightarrow 2|x \Leftrightarrow x=2x_1$ . Подставляем:
$x^2=2y^2 \Leftrightarrow 4x_1^2=2y^2 \Leftrightarrow 2x_1^2=y^2 \Rightarrow 2|y^2 \Rightarrow 2|y \Leftrightarrow y=2y_1$ . Подставляем:
$2x_1^2=y^2 \Leftrightarrow 2x_1^2=4y_1^2 \Leftrightarrow x_1^2=2y_1^2$ - получили исходное уравнение.
Таким образом, мы получили, что если $$(x,y)$$

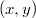
- решение уравнения $$x^2=2y^2$$

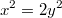
, то

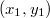
- тоже решение уравнения $$x^2=2y^2$$

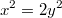
, причем $|x_1| = \frac{|x|}{2} <|x|, |y_1| = \frac{|y|}{2} < |y|$ . Повторяя процедуру достаточное количество раз по индукции придем к существованию натуральнозначного решения $$(x_k,y_k)$$

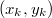
, которое меньше, чем 1, но при этом положительно. Однако тогда решение не может быть натуральнозначным. Противоречие. Таким образом $$(0;0)$$

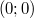
- единственное решение данного уравнения.

В общем случае соотношения между $$x$$

и

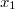
могут быть довольно сложными (например, так обстоит дело при решении методом спуска уравнения $$y^2=x^3+1$$

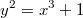
). Может быть и так, что спуск приводит к противоречию лишь при $x \geqslant x_0$ , а при $$x<x_0$$

вполне могут быть решения. Так что в общем случае одним "аналогично сокращаем" не отделаешься.

yourdomain.com