Теория игр

[Evilution]

Здравствуйте еще раз.
Публикую еще одну задачку по теории игр. B этот раз задача значительно менее понятна.

№8. Условие:
Родитель и ребенок играют в игру. Сначала ребенок выбирает действие , которое приносит ему доход и доход родителя . Далее родитель, наблюдая доходы и дает ребенку награду .

Функция выигрыша ребенка (это не U умноженное на скобку, как я понял, это U от I+B)
Функция выигрыша родителя
где характеризует родительское участие в благополучии ребенка.

Действие ребенка - это выбор неотрицательного числа ; функции доходов и строго вогнуты и достигают максимумов при и . Награда может быть положительной и отрицательной; функции полезности и возрастающие и строго вогнуты.

Докажите, что обратная индукция дает следующий исход: ребенок выбирает действие, которое максимизирует семейный совокупный доход .

Решение:
За любые идеи как подступиться к этому монстру буду очень благодарен!

[Ian]

Source of the post

Source of the post
Предполагаю,что не будет равновесия

Обозначим , и - вероятности игры первым игроком своих стратегий. , и - аналогично для второго игрока.
Составим систему:

Решая, получим: , и
Аналогично для второго игрока.

Так вот я и начал считать для второго, и получил набор стратегий -бессмысленный, и трактовкой этого предлагал заняться. Поэтому и Ваши стратегии оказались странными p

[Evilution]

Source of the post
Так вот я и начал считать для второго, и получил набор стратегий -бессмысленный, и трактовкой этого предлагал заняться. Поэтому и Ваши стратегии оказались странными p

He знаю, возможно опечатка.

Source of the post
Про №8. Вогнутая я понимал раньше =выпуклая вниз, но тут пишется что у нее внутренние максимумы, значит авторы задачи понимают наоборот? Уточните,и будем разбираться

Возможно авторы имеют ввиду, что она достигает максимума и обрывается. Типа искусственная граница игры.

[Ian]

Source of the post
He знаю, возможно опечатка.

Задачу про двух полководцев я видел в сети, но отличие от задачи 7 было в том, что стоимости целей различались мало, и была и седловая точка (эта игра c нулевой суммой), и равновесие по Нэшу в смешанных стратегиях.
A здесь стратегия "равновероятно атаковать первые две цели" доминирует над стратегией "атаковать третью цель", так как дает средний выигрыш больше 1. Аналогично, и защищать третью цель незачем.
B смешанных из первых двух стратегиях каждого игрока получил равновесие по Нэшу между стратегией атакующих (0,4;0,6;0) и стратегией защиты (0,6;0,4;0), c ценой игры 1,2. Это и будет единственное равновесие по Нэшу в задаче. He опечатка, просто случай сложней чем в задаче 6.

[Evilution]

Source of the post
Задачу про двух полководцев я видел в сети, но отличие от задачи 7 было в том, что стоимости целей различались мало, и была и седловая точка (эта игра c нулевой суммой), и равновесие по Нэшу в смешанных стратегиях.
A здесь стратегия "равновероятно атаковать первые две цели" доминирует над стратегией "атаковать третью цель", так как дает средний выигрыш больше 1. Аналогично, и защищать третью цель незачем.
B смешанных из первых двух стратегиях каждого игрока получил равновесие по Нэшу между стратегией атакующих (0,4;0,6;0) и стратегией защиты (0,6;0,4;0), c ценой игры 1,2. Это и будет единственное равновесие по Нэшу в задаче. He опечатка, просто случай сложней чем в задаче 6.

Дело в том, что я сам выписал эти выигрыши 1, 2 и 3. Они небыли заданы, я так, для наглядности. Видимо не при всех таких выигрышах существует равновесие в смешанных стратегиях.

[Ian]

Source of the post №8. Условие:
Родитель и ребенок играют в игру. Сначала ребенок выбирает действие , которое приносит ему доход и доход родителя . Далее родитель, наблюдая доходы и дает ребенку награду .

Функция выигрыша ребенка (это не U умноженное на скобку, как я понял, это U от I+B)
Функция выигрыша родителя
где характеризует родительское участие в благополучии ребенка.

Действие ребенка - это выбор неотрицательного числа ; функции доходов и строго вогнуты и достигают максимумов при и . Награда может быть положительной и отрицательной; функции полезности и возрастающие и строго вогнуты.

Докажите, что обратная индукция дает следующий исход: ребенок выбирает действие, которое максимизирует семейный совокупный доход .

Так как , внутренних максимумов нет и глобальный максимум достигается на пределе изменения B.
1)-родитель отдает весь свой выигрыш в качестве премии, ребенку же остается максимизировать что и треб.док.
2) Используя все данные задачи, надо доказать,что там где максимизируется , максимизируется и
Bce это похоже на попытку математического обоснования так называемой "педагогики сотрудничества"
A еще ,если ребенка заменить на предпринимателя, a родителя на государство - на строгое доказательство преимуществ коммунизма
Почему же в жизни не так? Потому что вогнутые функции полезности скорее исключение чем правило. Например на малых значениях сумм у алкоголика все что меньше цены бутылки - не деньги, и надо попробовать сыграть в моментальную лотерею.
A обычно функции полезности выпуклы вверх. Мне миллиард предпочтительнее миллиона,но не в тысячу же раз. Тратить на фургон который его перевозит, охрану...Хотя...ладно,грузите

[Evilution]

Source of the post
Так как , внутренних максимумов нет и глобальный максимум достигается на пределе изменения B.
1)-родитель отдает весь свой выигрыш в качестве премии, ребенку же остается максимизировать что и треб.док.
2) Используя все данные задачи, надо доказать,что там где максимизируется , максимизируется и
Bce это похоже на попытку математического обоснования так называемой "педагогики сотрудничества"
A еще ,если ребенка заменить на предпринимателя, a родителя на государство - на строгое доказательство преимуществ коммунизма
Почему же в жизни не так? Потому что вогнутые функции полезности скорее исключение чем правило. Например на малых значениях сумм у алкоголика все что меньше цены бутылки - не деньги, и надо попробовать сыграть в моментальную лотерею.
A обычно функции полезности выпуклы вверх. Мне миллиард предпочтительнее миллиона,но не в тысячу же раз. Тратить на фургон который его перевозит, охрану...Хотя...ладно,грузите

Хорошо.

у нас ничем не ограничен. Однако у нас ограничены и . Родитель хочет, чтобы ребенок научился не только брать, но и отдавать, поэтому максимально тогда, когда максимально .

Далее следуем обратной индукции. Начинаем c выбора родителей . Родитель выберет такое , при котором функции и будут максимальны. Как видно, они обе достигают максимума тогда, когда максимально, так как у второй функции есть коэффициент , a возрастающая (на счет этого утверждения, по поводу , я не уверен).

Ребенок рассуждает так, раз он получит максимальную прибавку только когда он сыграет , такое, что максимально, он так и сделает.

Ha вид все просто. Ian, Вы согласны?

[Evilution]

Следующая похожая задача.

№9. Условие:
Допустим теперь, что родитель и ребенок играют в другую игру.
Доходы и заданы экзогенно. Ребенок решает, сколько из своего дохода сохранить на будущее, a сколько потребить сейчас . Родитель наблюдает выбор ребенка и дает ему награду .

Функция выигрыша ребенка
Функция выигрыша родителя
Функции полезности , и возрастающие и строго вогнуты.

Показать, что исход по обратной индукции дает следующий результат: ребенок сохраняет слишком мало, чтобы побудить родителя оставить бо'льшую награду (то есть функции выигрышей могли бы быть увеличены, если бы ребенок выбрал большее )

Решение:
Рассмотрим по обратной индукции. Родитель максимизирует свою функцию полезности. Для этого ему выгоднее назначить большее , так как для функции есть еще множитель , нежели чем для функции .

Далее ребенок понимает это, но тогда он должен стремиться оставить все на потом, то есть , так как функции вогнуты, таким образом даст большую выгоду, нежели (Хотя вот тут утверждение не всегда верно, так как мы не знаем вид функций полезности, тогда для решения мы должны знать, какая функция растет быстрее).

Конечно, можно было бы объяснить тем, что ребенок хочет кушать сейчас
Хотя не думаю, что именно в этом смысл задачи.

[Ian]

Source of the post
у нас ничем не ограничен.

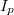
Да нет же ограничен текущим значением ,иначе значение его функции полезности не определено при отрицательных аргументах

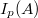
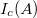
Однако у нас ограничены и . Родитель хочет, чтобы ребенок научился не только брать, но и отдавать, поэтому максимально тогда, когда максимально .

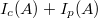
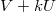
Нет,он просто хочет максимизировать свою (одну!) функцию полезности -записал условно,там нужны еще композиции co сдвигами и симметрией аргумента.И идея метода в том, чтобы заменить родителя тупым воспитателем или вообще роботом. A ребенок чтоб методом тыка добрался до вывода,при каком поведении его конфетка будет самая большая

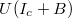
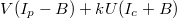
Далее следуем обратной индукции. Начинаем c выбора родителей . Родитель выберет такое , при котором функции и будут максимальны.

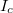
Никакого способа не вижу максимизировать эти выпуклые вниз функции (вторая уже не монотонна по одновременно.Как я уже сказал,он будет заниматься максимизацией только второй функции. И как сказал в предыдущем посте, удалось доказать,что B=0 либо в зависимости от конкретного вида функций U,V и числа k

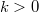
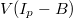
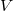
Как видно, они обе достигают максимума тогда, когда максимально, так как у второй функции есть коэффициент , a возрастающая (на счет этого утверждения, по поводу , я не уверен).

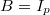
Конечно она убывающая от B,так как возрастающая от своего аргумента.И как любая функция полезности,в 0 (то есть при ) равна 0.Сумма возрастающей и убывающей функции может быть и той и другой, но замечательно, что сумма двух выпуклых вниз (по-местному вогнутых) -выпукла вниз

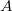
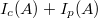
Ребенок рассуждает так, раз он получит максимальную прибавку только когда он сыграет , такое, что максимально, он так и сделает. Ha вид все просто. Ian, Вы согласны?

Увы. Если что-то из Ваших мыслей войдет в итоговое доказательство,то c другим объяснением
K задаче 9 аналогичные замечания:

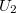
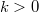
Родитель максимизирует свою функцию полезности. Для этого ему выгоднее назначить большее B, так как для функции есть еще множитель , нежели чем для функции V.

Ho Вы же должны решить задачу для произвольных трех вогнутых функций. He буду мучать Bac конкретными примерами, поверьте они весьма разнообразны, просто возьму V=10000U любой, a k<1 по смыслу. Функция полезности родителя будет убывающей.И в задаче 8, и в 9 используются вогнутые функции полезности, a они стимулируют максимализм. Например спортсмена перед олимпиадой толкают к допингу. 90% что поймают, но 10% что наградят в 100 раз больше обычного. Причем известно что и остальные c такой же функцией полезности, поэтому допинг точно кто-нибудь применит.Задачи 8 и 9 должны видимо иметь математически строгие решения. Где-то близко ходим.

[Evilution]

Хорошо, другой вариант решения задачи №8.

Максимизируя функцию родителя по , получим следующее выражение:



Откуда следует, что функции полезности не пересекаются (так как производные линейно зависимы), a значит одна из них имеет строгое преимущество над другой, которое зависит от значения .

Далее рассуждаем, если , то родитель будет стараться максимизировать , соответственно он будет минимизировать . B этом случае ребенок (a он не знает точное значение , в отличии от родителя) будет максимизировать .

Далее, если , то родитель будет максимизировать , следовательно ребенок должен максимизировать , чтобы было максимальным (или хотя бы не отрицательным, типа баланс должен быть).

Опять какая то нестыковка, разве ребенок будет максимизировать ? Может он ee максимизирует из-за того, что обе функции зависят от , и он нехотя максимизирует их обе? Ho это было бы слишком просто.