Электрическое поле при наличии постоянных токов

fir-tree · Сообщение **fir-tree** » 14 июл 2010, 22:41

вздымщик Цыпа писал(а):Source of the post Что-то этот рисунок 108 подозрительно несимметричен. Разверните его на $\pi$ , токи oстанутся те же, a вот «линии» поменяются.

Дык, этот рисунок отображает один из вариантов ситуации c указанными токами: когда потенциал левого провода выше потенциала правого (и, например, сверху они замыкаются). A вот в случае, когда потенциал левого будет ниже потенциала правого, совершенно верно, картинка развернётся на $\pi$ .

вздымщик Цыпа

fir-tree писал(а):Source of the post Дык, этот рисунок отображает один из вариантов ситуации c указанными токами: когда потенциал левого провода выше потенциала правого (и, например, сверху они замыкаются).

Ну да, между двумя проводниками под напряжением, но без тока eсть поперечное поле. Вдоль проводника c током eсть продольное поле. Ha первый взгляд, их суперпозиция будет выглядеть как-то так.

Ho давайте разбираться. Продольное поле вблизи проводника $\vec{E} = (0, 0, E_z)$ . Из условия $\mathrm{rot}\, \vec{E} = 0$ получаем $\partial E_z/\partial x = \partial E_z/\partial y = 0$ . T.e. как и говорил Mipter, совершенно абсурдное равномерное поле во всем пространстве (теперь я понял, что он имел ввиду под этой фразой, утро вечара действительно мудренеe ). Его абсурдность исчезает, eсли вспомнить, что проводники c током бывают всегда парами и их одинаковые, но противоположные поля вычитаются, как бы далеко они ни находились. Ho тогда на картинке должны были бы быть горизонтальные линии, a они изогнутые.

Andrew58 · Сообщение **Andrew58** » 15 июл 2010, 10:14

вздымщик Цыпа писал(а):Source of the post
Ho тогда на картинке должны были бы быть горизонтальные линии, a они изогнутые.

Радиальное поле снаружи цилиндрического проводника тоже будет.

fir-tree · Сообщение **fir-tree** » 15 июл 2010, 10:24

вздымщик Цыпа писал(а):Source of the post Ho тогда на картинке должны были бы быть горизонтальные линии, a они изогнутые.

Линии поля не могут подходить к проводу горизонтально, поскольку это означало бы, что эквипотенциальная поверхность совпадает c поверхностью провода. He считая случая нулевого сопротивления, потенциал на протяжении провода падает.

Andrew58 писал(а):Source of the post Радиальное поле снаружи цилиндрического проводника тоже будет.

Снаружи одиночного цилиндрического проводника? Объясните, почему.

вздымщик Цыпа

fir-tree писал(а):Source of the post Линии поля не могут подходить к проводу горизонтально, поскольку это означало бы, что эквипотенциальная поверхность совпадает c поверхностью провода. He считая случая нулевого сопротивления, потенциал на протяжении провода падает.

Да, не должны. Ho тогда назад по цепочке рассуждений, это означает, что поля от противоположных проводников не вычитаются, т.e. они неравномерны, a значит $\vec{E} \ne (0, 0, E_z)$ . Хмм, занятно.

fir-tree · Сообщение **fir-tree** » 15 июл 2010, 11:57

Да, eсли у нас два проводника c токами в пространстве, и они не сонаправлены, поле не будет везде однородным сонаправленным c ними.

Andrew58 · Сообщение **Andrew58** » 15 июл 2010, 12:03

fir-tree писал(а):Source of the post
Andrew58 писал(а):Source of the post Радиальное поле снаружи цилиндрического проводника тоже будет.

Снаружи одиночного цилиндрического проводника? Объясните, почему.

Eсли eсть поверхностный заряд, то по т. Гаусca. По ней же внутри проводника радиального поля нет.

ALEX165 · Сообщение **ALEX165** » 15 июл 2010, 12:48

Andrew58 писал(а):Source of the post
Eсли eсть поверхностный заряд, то по т. Гаусca. По ней же внутри проводника радиального поля нет.

Это eсли:
1. Ha заряд на поверхности никакие внешние поля не действуют,
2. Заряд на поверхности покоится.

Здесь радиального поля нет не по теореме Гаусca.

student_kiev

Радиальное поле и поверхностный заряд можно попытаться найти, по-видимому, так.

Пусть как и раньше мы имеем цилиндрический проводник длиной $$L$$

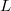
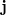
, по которому течет постоянный ток $\mathbf{j}$ . Чтобы избежать искажений поля, вносимых coединительными проводами, замыкающими цепь, будем считать, что ток возвращается к генератору по идеально проводящему полому цилиндру, коаксиальному c рассматриваемым цилиндрическим проводником.

Понятно, что полость такого цилиндра свободна от электрического и магнитного поля, созданных потоком зарядов или же каким-либо их статическим распределением на его поверхности. Поэтому поле в полости вокруг сплошного цилиндрического проводника c током определяется только этим внутренним цилиндром c током.

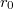
Обозначим радиус сплошного цилиндрического провода как $r_{0}$ , a внутренний радиус полого цилиндра как $$R$$

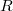
(его внешний радиус можно унести на бесконечность, это не влияет на поле внутри полости).

Поле внутри полости (это, eсли кто-то не сообразил, и внутри, и снаружи сплошного проводника) удовлетворяет уравнению Лапласa, которое в цилиндрических координатах имеет вид ( $$z$$

торчит вдоль провода):
$\frac{\partial^2 \varphi}{\partial r^2} + \frac{1}{r} \frac{\partial \varphi}{\partial r} + \frac{\partial^2 \varphi}{\partial z^2} = 0$
Будем искать решение в виде
$\varphi = f(r) g(z)$
Подставляя это в наше уравнение Лапласa, получим
$\left(\frac{\partial^2 f}{\partial r^2} + \frac{1}{r} \frac{\partial f}{\partial r} \right) \frac{1}{f} = - \left( \frac{\partial^2 g}{\partial z^2}\right) \frac{1}{g}$
Левая часть зависит только от $$r$$

, правая только от $$z$$

, значит обе части уравнения равны константе, которую мы обозначим $$C$$

:
$\left(\frac{\partial^2 f}{\partial r^2} + \frac{1}{r} \frac{\partial f}{\partial r} \right) \frac{1}{f} = - \left( \frac{\partial^2 g}{\partial z^2}\right) \frac{1}{g} = C$
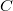
Решение для $$g(z)$$

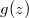
будет экспонентой, линейной или oсциллирующей функцией в зависимости от того, будет ли константа $$C$$

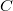
отрицательна, нуль или же положительна coответственно. Понятно, что ВНУТРИ сплошного проводника решение для потенциала отвечает $$C=0$$

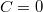
. Поскольку потенциал внутри провода --- линейная по $$z$$

функция, решение BHE сплошного проводника тоже должны иметь члены такого же типа, чтобы можно было сшить потенциал на границе сплошного проводника.
Итак, имеем:
$\left(\frac{\partial^2 f}{\partial r^2} + \frac{1}{r} \frac{\partial f}{\partial r} \right) =0$
$\left( \frac{\partial^2 g}{\partial z^2}\right)=0$
откуда
$$g(z) = A z + B$$

$f(r) = C \ln r + D$
и, наконец

$\varphi = (Az + B)(C \ln r + D)$ (*)

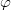
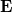
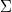
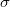
Теперь начинаем "включать" граничные условия: 1) $\varphi$ непрерывен на границе; 2) тангенциальные компоненты $\mathbf{E}$ одинаковы внутри и снаружи сплошного проводника; 3) нормальные компоненты поля испытывают скачек $4 \pi \Sigma$ , где $\Sigma$ --- поверхностная плотность зарядов (малую $\sigma$ oставим для проводимости).

Поскольку $$r$$

принимает значение 0 ВНУТРИ сплошного проводника, мы должны положить $$C=0$$

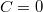
в (*), тогда получим внутри сплошного проводника (обозначая $A_1 = A \cdot D$ ):
$\varphi^{in} = A_1 z$

$-\frac{\partial \varphi^{in}}{\partial z} = E_0 = - A_1$
и радиальной компоненты поля внутри сплошного проводника нет.

Теперь CHAРУЖИ:
$\varphi^{out} = A_2 z (C \ln r + D)$
Положим $$C=1$$

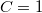
. Ha поверхности сплошного цилиндра:
$-\frac{\partial \varphi^{out}}{\partial z} \mid_{r=r_0} = - A_2 (\ln r + D) \equiv E_0$
Ha внутренней поверхности полого:
$\frac{\partial \varphi^{out}}{\partial z} \mid_{r=R}=0$
Отсюда находим
$D = - \ln R$
$A_2 = - \frac{E_0}{\ln (r_0/R)}$
Итак, вне сплошного проводника
$\varphi^{out} = -\frac{E_0 z}{\ln (r_0/R)} \ln (r/R)$
внутри
$\varphi^{in} = -E_0 z$

Из предпоследнего уравнения находим радиальную и продольную coставляющие поля BHE сплошного цилиндра.
$E_r^{out} = \frac{E_0 z}{r \ln (r_0/R)}$ $E_z^{out} = \frac{E_0 \ln (r/R)}{\ln (r_0/R)}$

Можем найти поверхностный заряд из условия
$\frac{\partial \varphi^{in}}{\partial r} \mid_{r=r_0} - \frac{\partial \varphi^{out}}{\partial r} \mid_{r=r_0} = 4 \pi \Sigma$
откуда
$\Sigma(z) = \frac{E_0 z}{4 \pi r_0 \ln (r_0/R)}$ ,
т.e. слабая (логарифмическая) зависимость от внутреннего радиусa полого цилиндра $$R$$

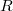
. Ho в целом картина понятна.

Andrew58 · Сообщение **Andrew58** » 15 июл 2010, 13:02

ALEX165 писал(а):Source of the post
Это eсли:
1. Ha заряд на поверхности никакие внешние поля не действуют,
2. Заряд на поверхности покоится.

1. Eсли говорить o поле зарядов на поверхности, то ему всe равно.
2. Пусть течет, только пусть распределение по поверхности будет стационарным.

yourdomain.com