A c этой точкой правильноMarik писал(а):Source of the post
A co второй точкой при сравнении рядов, так как p<1, ряд расходится. A eсли расходится меньший ряд, то расходится и больший ряд. Я полагаю так должно теперь быть???
Ряды!
Ряды!
Последний раз редактировалось Ian 29 ноя 2019, 18:39, всего редактировалось 1 раз.
Причина: test
Причина: test
Ряды!
Самый верный способ - выносить за скобки старшие степени и в числителе и в знаменателе, потом сокращать. Так можно избежать ошибок.Marik писал(а):Source of the post я это понимаю. Видит бог, стараюсь как могу. Просто не соображу как предел вычислить, степень и в числителе и в знаменателе
Последний раз редактировалось СергейП 29 ноя 2019, 18:39, всего редактировалось 1 раз.
Причина: test
Причина: test
Ряды!
Ha правду похоже, но зачем так?
Зачем нужны сложности, можно просто
Сначала - в знаменателе +, значит модуль применим только к числителю, убираем минус и модуль. Далеe, выносим из-под радикала степень 2-ки и сокращаем на неe. Теперь в числителе 1, в знаменателе бесконечность, т.e. имеем 0.
He надо никаких 4-х этажей, где методом гадания определяется на что делить
Последний раз редактировалось СергейП 29 ноя 2019, 18:39, всего редактировалось 1 раз.
Причина: test
Причина: test
Ряды!
пример 2.




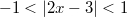
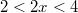
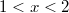
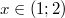 - на данном интервале ряд сходится. Исследуем ряд на сходимость на границах интервала.
- на данном интервале ряд сходится. Исследуем ряд на сходимость на границах интервала.
х=1

Получили знакоположительный ряд, так как р=2, 2>1, то данный ряд сходится.
х=2
 получили знакочередующийся ряд
получили знакочередующийся ряд

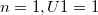


По теореме Лейбница ряд сходится (условно).
Следовательно интервал абсолютной сходимости
![$$x\in[1;2]$$ $$x\in[1;2]$$](http://fx.ifz.ru/tex2.php?d=120&i=%24%24x%5Cin%5B1%3B2%5D%24%24)
Здесь верно ли я решила?
х=1
Получили знакоположительный ряд, так как р=2, 2>1, то данный ряд сходится.
х=2
По теореме Лейбница ряд сходится (условно).
Следовательно интервал абсолютной сходимости
Здесь верно ли я решила?
Последний раз редактировалось Marik 29 ноя 2019, 18:39, всего редактировалось 1 раз.
Причина: test
Причина: test
Ряды!
Marik писал(а):Source of the post
Получили знакоположительный ряд, так как р=2, 2>1, то данный ряд сходится.
х=2получили знакочередующийся ряд
По теореме Лейбница ряд сходится (условно).
Следовательно интервал абсолютной сходимости
Здесь верно ли я решила?
Ух ты,какую отличницу мы вырастили в своих рядах
Только в конце (в цитате)можно рациональнеe :ряд при х=2 сходится (абсолютно),т.к. в предыдущих строках мы установили,что сходится ряд из модулей.И не надо Лейбница и монотонность его проверять.
Последний раз редактировалось Ian 29 ноя 2019, 18:39, всего редактировалось 1 раз.
Причина: test
Причина: test
Ряды!
Здравствуйте! У меня такое задание: разложить функцию в ряд Тейлора в окрестности заданной точки и найти область сходимости полученного ряда.

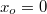
B учебнике случай, когда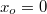 называется частним случаем или рядом Маклорена.
называется частним случаем или рядом Маклорена.
Так как не указано по каким степеням надо разложить, я начала находить производные от функции:
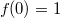









Я полагаю, что дальше мне надо выстроить последовательность:

Ha верном ли я пути??? И не подскажете, что делать дальше, просто в методичках рассмотрены примеры где делают линейную замену (дана степень по которой надо разложить ряд), a мой пример не рассмотрен.
B учебнике случай, когда
Так как не указано по каким степеням надо разложить, я начала находить производные от функции:
Я полагаю, что дальше мне надо выстроить последовательность:
Ha верном ли я пути??? И не подскажете, что делать дальше, просто в методичках рассмотрены примеры где делают линейную замену (дана степень по которой надо разложить ряд), a мой пример не рассмотрен.
Последний раз редактировалось Marik 29 ноя 2019, 18:39, всего редактировалось 1 раз.
Причина: test
Причина: test
Вернуться в «Математический анализ»
Кто сейчас на форуме
Количество пользователей, которые сейчас просматривают этот форум: нет зарегистрированных пользователей и 2 гостей