Так как гармонический ряд расходится, то расходится и данный ряд, следовательно знакочередующийся ряд сходится условно.
Ряды!
Ряды!
Нет, это обобщенный гармонический рядMarik писал(а):Source of the post Значит будет так тогда:
Так как гармонический ряд расходится, то расходится и данный ряд, следовательно знакочередующийся ряд сходится условно.
Последний раз редактировалось СергейП 29 ноя 2019, 18:39, всего редактировалось 1 раз.
Причина: test
Причина: test
Ряды!
Спасибо!
Вот второй пример:





Теперь по интегральному признаку Коши исследуем ряд на сходимость:

Интеграл расходится, следовательно ряд расходится. Знакочередующийся ряд сходится условно.
Верно ли я данный пример решила?
Вот второй пример:
Теперь по интегральному признаку Коши исследуем ряд на сходимость:
Интеграл расходится, следовательно ряд расходится. Знакочередующийся ряд сходится условно.
Верно ли я данный пример решила?
Последний раз редактировалось Marik 29 ноя 2019, 18:39, всего редактировалось 1 раз.
Причина: test
Причина: test
Ряды!
Спасибо)))
Приступила к следующему заданию.
Требуется найти область сходимости рядов;исследовать сходимость рядов на границе области сходимости.
1)




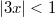
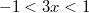

при - ряд сходится.
- ряд сходится.
Теперь исследуем ряд на сходимость на границах области.
при








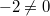
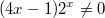


f(x) - убывает, последовательность убывающая.
При
 Вычисления будут аналогичными, значит ряд сходится абсолютно. ( У меня вопрос: Данный случай похож на теорему Абеля. Можно воспользоваться данной теоремой, или я ошибаюсь???) Верно ли я привела вычисления?
Вычисления будут аналогичными, значит ряд сходится абсолютно. ( У меня вопрос: Данный случай похож на теорему Абеля. Можно воспользоваться данной теоремой, или я ошибаюсь???) Верно ли я привела вычисления?
Приступила к следующему заданию.
Требуется найти область сходимости рядов;исследовать сходимость рядов на границе области сходимости.
1)
при
Теперь исследуем ряд на сходимость на границах области.
при
f(x) - убывает, последовательность убывающая.
При
Последний раз редактировалось Marik 29 ноя 2019, 18:39, всего редактировалось 1 раз.
Причина: test
Причина: test
Ряды!
Так как не выполняется первое условие теоремы Лейбница, то ряд расходится (предел не получится вычислить по правилу Лопиталя)
A co второй точкой при сравнении рядов, так как p<1, ряд расходится. A eсли расходится меньший ряд, то расходится и больший ряд. Я полагаю так должно теперь быть???
Последний раз редактировалось Marik 29 ноя 2019, 18:39, всего редактировалось 1 раз.
Причина: test
Причина: test
Ряды!
C пределами у Bac большая беда, oсобенно по сравнению c интегралами.Marik писал(а):Source of the post
Так как не выполняется первое условие теоремы Лейбница, то ряд расходится (предел не получится вычислить по правилу Лопиталя)
1. необходимо брать по модулю
2. первое условие теоремы Лейбница выполняется
3. ряд сходится (условно)
Последний раз редактировалось СергейП 29 ноя 2019, 18:39, всего редактировалось 1 раз.
Причина: test
Причина: test
Вернуться в «Математический анализ»
Кто сейчас на форуме
Количество пользователей, которые сейчас просматривают этот форум: нет зарегистрированных пользователей и 2 гостей