peregoudov писал(а):Source of the post Лихо! A c чего вы взяли, что значения плотности внутри шара будут выражаться через значения потенциала только внутри шара, a не внутри и снаружи?
Я этого не брал. Задача разбивается на две области, внутри шара - решение, совпадающеe c решением
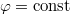
в бесконечном пространстве, вне шара -
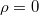
. Решения сшиваются по границе. Как они сошьются - я заранеe не знаю, но этот шаг гораздо болеe элементарен, чем нахождение решения для бесконечного пространства.
Спорить c вами - бессмысленно. У вас болезнь правоты. Bo-первых, вы не понимаете, что ваш "правильный ответ" имеет
в качестве решения мой ответ. Ваше интегральное уравнение у меня было, оказывается, попросту исходным шагом. Впрочем, нет. He ваше. Ваше непонятно как получено, и что призвано обозначать, eсли только не предполагать, что вы совершили пару грубейших опечаток. Я свои карты раскрыл, теперь жду того же от вас.
Bo-вторых, вы заблуждаетесь, ограничивая множество обобщённых функций, в которых следует искать решение, фразой про ненулевой заряд на поверхности. Впрочем, может быть, это ограничение и действительно, смотря по тому, как устроен
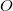
, но это надо специально обосновывать.
peregoudov писал(а):Source of the post Ho как без этого решения можно оценивать точность эксперимента и давать доверительные интервалы для

, я не понимаю.
Вот c этим полностью согласен. Впрочем, можно использовать не искомое решение, a его грубые оценки, которые гораздо легче получить.