yourdomain.com

Найти все целые значения $$a$$

при которых $x^{13}+x+90$ делится на $$x^2 - x+a$$

bot писал(а):Source of the post
Найти все целые значения при которых $x^{13}+x+90$ делится на

Сразу видно, что $$ a | 90 $$

. Значит,

$a \in \{\pm 1,\ \pm 2,\ \pm 3\ \pm 5,\ \pm 6,\ \pm 9,\ \pm 10,\ \pm 15,\ \pm 18,\ \pm 30,\ \pm 45,\ \pm 90}$ .

Можно проверить все 24 варианта, a можно сделать проще. Перейдем к многочленам по модулю 3. Получим, что $x^{13} + x \equiv 0\ \pmod{x^2 + 2x + a}$ . Это возможно,только если $a \equiv 2\ \pmod{3}$ . Следовательно, у нас осталось только 4 варианта:
$a \in \{-10,\ -1,\ 2,\ 5 \}$ ,
которые и нужно проверить.

Можно перейти и к многочленам по модулю 5. Тогда получим

$x (x^{12} + 1) \equiv 0\ \pmod{x^2 + 4x + a}$ .

Отсюда следует, что если $a \equiv 0\ \pmod{5}$ или если $a \equiv 4\ \pmod{5}$ , то сравнение не выполняется. Значит, у нас остается единственный вариант $$ a = 2 $$

.

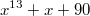Пусть многочлен $x^{13}+x+90$ делится на $$x^2-x+a$$

, где

- целое число, тогда
$x^{13}+x+90=(x^2-x+a)\cdot f(x),$
где многочлен $$f(x)$$

имеет целые коэффициенты (так как старший коэффициент многочлена $$x^2-x+a$$

равен 1).

Ввиду равенств $90=a\cdot f(0), 92=a\cdot f(1)$ получаем, что $$a|2$$

.

Так как $8284=(a+2)\cdot f(2), -8184=(a+6)\cdot f(-2)$ , то $$(a+2)|8284$$

и

. Значит,

не равно ни $$1$$

, ни

и не

.

Так как верно равенство $x^{13}+x+90=(x^2-x+2)\cdot(x^{11}+x^{10}-x^9-3x^8-x^7+5x^6+7x^5-3x^4-17x^3-11x^2+23x+45)$ , то получаем, что ответом задачи будет число 2.

Угу, я дважды ошибался пока делил. Однако проверить a=2 можно ещё парой способов.
1) Полагаем $x=\frac{1+\sqrt7i}{2}$ и последовательно вычислив $x^2, x^4, x^8, x^{12}=x^4x^8$ убеждаемся, что $x(x^{12}+1)+90=0$ .
По схеме Горнера здесь дольше будет.
2) Пусть $$x^2-x+2=0$$

. Тогда

$x^2=x-2 \Rightarrow x^4=x^2-4x+4 = x-2-4x+4 = -3x+2 \Rightarrow x^8=...=-3x-14 \Rightarrow$

$x^{12}=x^4x^8=(3x-2)(3x+14)=...=45x-46 \Rightarrow x^{13}+x+90=x(45x-45)+90=45(x^2-x+2)=0$

yourdomain.com

Делимость многочленов

Делимость многочленов

Делимость многочленов

Делимость многочленов

Делимость многочленов