IMC 2012. День 1
Problem 1.
Для каждого положительного целого пусть
пусть 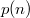 означает число способов представить
означает число способов представить  в виде суммы положительных целых чисел. Например,
в виде суммы положительных целых чисел. Например, 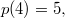 так как
так как 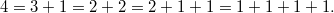 Также определим
Также определим 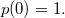
Докажите, что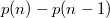 есть число способов представить
есть число способов представить  в виде суммы целых чисел, каждое из которых строго больше
в виде суммы целых чисел, каждое из которых строго больше 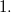
Problem 2.
Для каждого целого положительного определить наименьший возможный ранг матрицы
определить наименьший возможный ранг матрицы  , на главной диагонали которой стоят нули, а на остальных местах строго положительные действительные числа.
, на главной диагонали которой стоят нули, а на остальных местах строго положительные действительные числа.
Problem 3.
Дано Пусть
Пусть 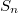 - группа перестановок чисел
- группа перестановок чисел 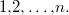 Двое игроков,
Двое игроков, 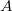 и
и  , играют в следующую игру. Делая ходы, они выбирают элементы (один элемент за раз) из группы
, играют в следующую игру. Делая ходы, они выбирают элементы (один элемент за раз) из группы 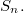 Запрещено выбирать элемент, который уже был выбран. Игра заканчивается, когда выбранные элементы порождают всю группу
Запрещено выбирать элемент, который уже был выбран. Игра заканчивается, когда выбранные элементы порождают всю группу 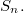 Игрок, который сделал последний ход, проигрывает. Первым ход делает
Игрок, который сделал последний ход, проигрывает. Первым ход делает 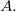 У кого из игроков есть выигрышная стратегия?
У кого из игроков есть выигрышная стратегия?
Problem 4.
Пусть непрерывно дифференцируемая функция, удовлетворяющая
непрерывно дифференцируемая функция, удовлетворяющая  для всех
для всех  Докажите, что
Докажите, что  для всех
для всех 
Problem 5.
Пусть - рациональное число, а
- рациональное число, а  - положительное целое. Докажите, что многочлен
- положительное целое. Докажите, что многочлен 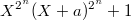 неприводим над кольцом многочленов с рациональными коэффициентами
неприводим над кольцом многочленов с рациональными коэффициентами ![$$\mathbb{Q}[X].$$ $$\mathbb{Q}[X].$$](http://fx.ifz.ru/tex2.php?d=120&i=%24%24%5Cmathbb%7BQ%7D%5BX%5D.%24%24)
Для каждого положительного целого
Докажите, что
Problem 2.
Для каждого целого положительного
Problem 3.
Дано
Problem 4.
Пусть
Problem 5.
Пусть