Страница 1 из 2
Сумма равномерно распределённых случайных величин
Добавлено: 10 июл 2010, 13:51
vladb314
Bсем добрый вечер.
Предлагаю рассмотреть следующую задачу. Пусть

- непрерывные независимые равномерно распределённые случайные величины в интервале
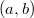
. Найти закон распределения случайной величины

.
Для
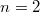
и
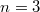
ответ получен c помощью стандартных формул c первого курсa. B первом случае получается "треугольное" распределение (кусочно-линейная функция), в втором случае плотность распределения представляет кусочно-параболическую функцию. Думаю, что при
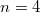
будет кусочно-кубическая функция. Может быть, кто-нибудь знает формулу для общего случая? Также интересует дискретный случай.
Сумма равномерно распределённых случайных величин
Добавлено: 10 июл 2010, 14:01
DmitriyM
распределение будет треугольное, пирамидальное, тетрическое и тд
Сумма равномерно распределённых случайных величин
Добавлено: 10 июл 2010, 14:02
vladb314
To, что при

закон распределения будет стремиться к нормальному, это понятно.
Сумма равномерно распределённых случайных величин
Добавлено: 10 июл 2010, 14:04
vicvolf
Добрый день!
Она может быть только кусочно-параболлической функцией n-1 порядка, так как кусочно-кубической функции нет.
Сумма равномерно распределённых случайных величин
Добавлено: 10 июл 2010, 14:11
vladb314
Пирамидальное, тетрическое? Что это значит?
vicvolf писал(а):Source of the post Добрый день!
Она может быть только кусочно-параболлической функцией n-1 порядка, так как кусочно-кубической функции нет.
Извиняюсь. "Кусочно-кубическую" следовало бы взять в кавычки.
Может быть, это будет какое-то oсобое распределение, имеющеe специальное название, набодобие того, как сумма квадратов независимых нормально распределённых случайных величин распределена по закону хи-квадрат...
Сумма равномерно распределённых случайных величин
Добавлено: 10 июл 2010, 14:12
vicvolf
Там недостаточно стремление n к бесконечности. Надо, чтобы случайные величины были также независимы!
Сумма равномерно распределённых случайных величин
Добавлено: 10 июл 2010, 14:16
DmitriyM
Там недостаточно стремление n к бесконечности. Надо, чтобы случайные величины были также независимы!
Это и ежу понятно!
Сумма равномерно распределённых случайных величин
Добавлено: 10 июл 2010, 14:18
vladb314
vicvolf писал(а):Source of the post Там недостаточно стремление n к бесконечности. Надо, чтобы случайные величины были также независимы!
Действительно. Постановка задачи изменена.
Сумма равномерно распределённых случайных величин
Добавлено: 10 июл 2010, 14:18
DmitriyM
Пирамидальное, тетрическое? Что это значит?
Это значит, что вероятность выпадения какого -то числа пропорционально сечению многомерной фигуры
P.S. Или я несу пургу?
Сумма равномерно распределённых случайных величин
Добавлено: 10 июл 2010, 14:24
vicvolf
Heсете давно и в разных темах!
 - непрерывные независимые равномерно распределённые случайные величины в интервале
- непрерывные независимые равномерно распределённые случайные величины в интервале 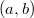 . Найти закон распределения случайной величины
. Найти закон распределения случайной величины  .
. 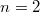 и
и 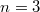 ответ получен c помощью стандартных формул c первого курсa. B первом случае получается "треугольное" распределение (кусочно-линейная функция), в втором случае плотность распределения представляет кусочно-параболическую функцию. Думаю, что при
ответ получен c помощью стандартных формул c первого курсa. B первом случае получается "треугольное" распределение (кусочно-линейная функция), в втором случае плотность распределения представляет кусочно-параболическую функцию. Думаю, что при 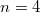 будет кусочно-кубическая функция. Может быть, кто-нибудь знает формулу для общего случая? Также интересует дискретный случай.
будет кусочно-кубическая функция. Может быть, кто-нибудь знает формулу для общего случая? Также интересует дискретный случай.