yourdomain.com

Известно, что если ряд является условно сходящимся, то при изменении порядка суммирования он может сходиться к любому другому числу.

Все перестановки абсолютно сходящегося ряда сходятся к одной и той же сумме.

Доказательство:

Для любого положительного $\epsilon$ существует такое N, что для всех $n \geq N$ выполняется
$|S-\sum_{i=1}^{n}{u_i}|<\epsilon$

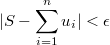
Пусть ряд
$\sum_{i=1}^{\infty}{w_i}$

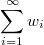
получен из ряда
$\sum_{i=1}^{\infty}{u_i}$
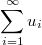
путем перестановки слагаемых

Возьмем число M таким, чтобы в сумму
$\sum_{i=1}^{M}{w_i}$

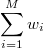
Входили все члены, входящие в сумму
$\sum_{i=1}^{N}{u_i}$

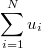
Запишем
$|S-\sum_{i=1}^{M}{w_i}|=|S-\sum_{i=1}^{M}{w_i}+\sum_{i=1}^{N}{u_i}-\sum_{i=1}^{N}{u_i}|$

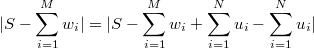
Отсюда получим
$|S-\sum_{i=1}^{M}{w_i}|=|(S-\sum_{i=1}^{N}{u_i})+(\sum_{i=1}^{N}{u_i}-\sum_{i=1}^{M}{w_i})|$

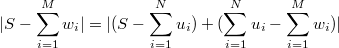
С учетом того, что модуль суммы меньше или равен сумме модулей
$|S-\sum_{i=1}^{M}{w_i}| \leq |S-\sum_{i=1}^{N}{u_i}|+|\sum_{i=1}^{N}{u_i}-\sum_{i=1}^{M}{w_i}|$

или

$|S-\sum_{i=1}^{M}{w_i}| \leq \epsilon +|\sum_{i=1}^{N}{u_i}-\sum_{i=1}^{M}{w_i}|$

Выбрав N достаточно большим, можно добиться того, что

$|\sum_{i=1}^{N}{u_i}-\sum_{i=1}^{M}{w_i}| \leq \epsilon$

То есть
$|S-\sum_{i=1}^{M}{w_i}| \leq 2\epsilon$

У меня такой вопрос: что в данном доказательсте делает его непригодным для случая, когда ряд не является абсолютно сходящимся

Mitry писал(а):Source of the post
У меня такой вопрос: что в данном доказательсте делает его непригодным для случая, когда ряд не является абсолютно сходящимся

Вот это:

Выбрав N достаточно большим, можно добиться того, что

$|\sum_{i=1}^{N}{u_i}-\sum_{i=1}^{M}{w_i}| \leq \epsilon$

Тут в любом случае надо еще долго доказывать, а для условно сходящегося так и неверно

Ian писал(а):Source of the post
Вот это:
Выбрав N достаточно большим, можно добиться того, что

$|\sum_{i=1}^{N}{u_i}-\sum_{i=1}^{M}{w_i}| \leq \epsilon$
Тут в любом случае надо еще долго доказывать

В это выражение дают вклад члены ряда u, номера которых больше, чем N. Если ряд сходится, то, выбрав N достаточно большим, можно добиться того, что

$|\sum_{i=N+1}^{\infty}{u_i}|<\epsilon$

Ian писал(а):Source of the post
а для условно сходящегося так и неверно

Вот я и хочу понять, почему.

Mitry писал(а):Source of the post В это выражение дают вклад члены ряда u, номера которых больше, чем N. Если ряд сходится, то, выбрав N достаточно большим, можно добиться того, что
$|\sum_{i=N+1}^{\infty}{u_i}|<\epsilon$

Этого-то можно добиться. А вот чтобы M-N из этих слагаемых, взятых не по порядку, в суиие были малы - не обязательно

Ian писал(а):Source of the post
Mitry писал(а):Source of the post В это выражение дают вклад члены ряда u, номера которых больше, чем N. Если ряд сходится, то, выбрав N достаточно большим, можно добиться того, что
$|\sum_{i=N+1}^{\infty}{u_i}|<\epsilon$
Этого-то можно добиться. А вот чтобы M-N из этих слагаемых, взятых не по порядку, в суиие были малы - не обязательно

Тогда получается, что требование абсолютной сходимости ряда необходимо для того, чтобы из соотношения
$\sum_{i=N+1}^{\infty}{|u_i|}<\epsilon$
следовала малость суммы любых любого количества этих слагаемых?

Mitry писал(а):Source of the post
Ian писал(а):Source of the post
Mitry писал(а):Source of the post В это выражение дают вклад члены ряда u, номера которых больше, чем N. Если ряд сходится, то, выбрав N достаточно большим, можно добиться того, что
$|\sum_{i=N+1}^{\infty}{u_i}|<\epsilon$
Этого-то можно добиться. А вот чтобы M-N из этих слагаемых, взятых не по порядку, в суиие были малы - не обязательно

Тогда получается, что требование абсолютной сходимости ряда необходимо для того, чтобы из соотношения
$\sum_{i=N+1}^{\infty}{|u_i|}<\epsilon$
следовала малость суммы любых любого количества этих слагаемых?

Из соотношения, как у Вас сейчас, с модулями -следует. А то которое было в предыдущем посте- ничего не дает

Условная сходимость равносильна сходимости + любой из трех вещей:
1) изменением нумерации членов можно заставить ряд сойтись к любой сумме, включая +- бесконечность, или чтобы предел частичных сумм не существовал ни в каком смысле.
2)не изменяя нумерацию , можно поменять знаки перед некоторыми членами ряда и добиться всего этого
3)можно вычеркнуть некоторые члены ряда и добиться этого же

yourdomain.com

Про сходимость рядов

Про сходимость рядов

Про сходимость рядов

Про сходимость рядов

Про сходимость рядов

Про сходимость рядов

Про сходимость рядов