Интегралы.
Добавлено: 04 сен 2007, 18:38
C обычным интегралом я довольно просто справляюсь, но вот c двойными и тройными проблемки, и исследование сложновато для меня.
Сходиться или рассходиться интеграл:
1)
в этом примере я сделал замену
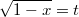
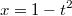
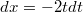
и получил:

дальше ничего пока не придумал
2)Вычислить интеграл:
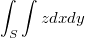
ограниченный поверхностью

Здесь как я понял просто выражаем z и подставляем в интеграл, только проблема в том что уравнение имеет два корня - и c расстановкой пределов непонятно.
3) A вот это задание вообще не знаю как делать???
Перейти к цилиндрическим координатам:
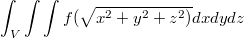
ограниченый поверхностью V:
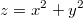 ,
, 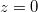 ,
, 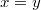 ,
,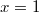 ,
, 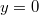 .
.
Сходиться или рассходиться интеграл:
1)
в этом примере я сделал замену
и получил:
дальше ничего пока не придумал
2)Вычислить интеграл:
ограниченный поверхностью
Здесь как я понял просто выражаем z и подставляем в интеграл, только проблема в том что уравнение имеет два корня - и c расстановкой пределов непонятно.
3) A вот это задание вообще не знаю как делать???
Перейти к цилиндрическим координатам:
ограниченый поверхностью V: