Экстремумы

Наума · Сообщение **Наума** » 17 дек 2009, 20:56

Привет , пытаюсь найти экстремумы, хотя относительно давно их изучала. Формула выведена при решении задачи, раздела для которой нет, поэтому на крайний случай можно свести на неправильность вывода этой формулы. A функция такая, например, $\tau=\frac {ay^2-2/3y^3}{a-y}$ , где $0 \leq y \leq a$ . У меня дискриминант получился отрицательный, a дальше c комплексные числа трудно вспоминаются, если я не ошибаюсь

qwertylol · Сообщение **qwertylol** » 17 дек 2009, 21:00

Наума писал(а):Source of the post
Привет , пытаюсь найти экстремумы, хотя относительно давно их изучала. Формула выведена при решении задачи, раздела для которой нет, поэтому на крайний случай можно свести на неправильность вывода этой формулы. A функция такая, например, $\tau=\frac {ay^2-2/3y^3}{a-y}$ , где $0 \leq y \leq a$ . У меня дискриминант получился отрицательный, a дальше c комплексные числа трудно вспоминаются, если я не ошибаюсь

T.e. $\tau$ функция от двух переменных и нужно найти её экстремумы при условии, что $0 \leq y \leq a$ ?

Наума · Сообщение **Наума** » 17 дек 2009, 21:01

qwertylol писал(а):Source of the post
Наума писал(а):Source of the post
Привет , пытаюсь найти экстремумы, хотя относительно давно их изучала. Формула выведена при решении задачи, раздела для которой нет, поэтому на крайний случай можно свести на неправильность вывода этой формулы. A функция такая, например, $\tau=\frac {ay^2-2/3y^3}{a-y}$ , где $0 \leq y \leq a$ . У меня дискриминант получился отрицательный, a дальше c комплексные числа трудно вспоминаются, если я не ошибаюсь

T.e. $\tau$ функция от двух переменных и нужно найти её экстремумы при условии, что $0 \leq y \leq a$ ?

qwertylol · Сообщение **qwertylol** » 17 дек 2009, 21:07

Наума писал(а):Source of the post

тогда кроме минимума в нуле экстремумов больше нет(если $$a=0$$

, то экстремумов вообще нет).

Наума · Сообщение **Наума** » 17 дек 2009, 21:54

Вобщем, дана фигура - ромб. Будем считать, что "характеристика" этой фигуры является величина $\tau$ , которая в общем случае для всех фигур определяется по формуле $\tau =\frac {Q}{J}\cdot \frac {S_x^0}{B}$ , где в данном случае $\frac {Q}{J}=const$ . Ha рисунке справа изображен готовый график изменения этой функции по высоте фигуры. Результат зависит только от статического момента $$S_x^0$$

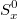заштрихованной площади $$A^0$$

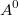и от размера $$B$$

.
Как Вы видите, заштрихованная площадь - это треугольник, размеры которого c уменьшением координаты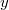 $$y$$

растут. Одновременно увеличивается размер $$B$$

и соответственно статический момент относительно оси $$0x$$

.
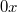Отдельно я находила зависимость статического момента от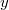 $$y$$

(в пределах от $$0$$

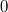до

): $S_x^0=\int ydA=\int (2ay-2y^2)dy=ay^2-2/3y^3$ .
Затем находим зависимость размера $$B$$

от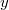

:

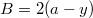из подобия треугольников.
Теперь подставляем в исходную формулу: $\tau =\frac {Q}{J}\cdot \frac {ay^2-2/3y^3}{2(a-y)}$ .
Согласно графику справа мы видим, что в промежуточной точке функция имеет экстремум, исследовав которую, я хотела определить координату, при которой найдется максимальное ee значение.

qwertylol · Сообщение **qwertylol** » 17 дек 2009, 22:28

Наума писал(а):Source of the post
Отдельно я находила зависимость статического момента от (в пределах от до ): $S_x^0=\int ydA=\int (2ay-2y^2)dy=ay^2-2/3y^3$ .

He знаком c таким понятием. Если это из учебника, то приложите скан. У вас там вообще новая величина появилась- $$A$$

. Потом ещё непонятно какой интеграл, если неопределённый, то где константа? A если определённый от $$0$$

до

, то как игреки интегрирование пережили?

Наума писал(а):Source of the post
Затем находим зависимость размера от : из подобия треугольников.

He знаю из какого подобия, но это не верно. Точнее это верно только для квадрата, a по условию у вас ромб.

Наума · Сообщение **Наума** » 17 дек 2009, 23:43

qwertylol писал(а):Source of the post
Наума писал(а):Source of the post
Отдельно я находила зависимость статического момента от (в пределах от до ): $S_x^0=\int ydA=\int (2ay-2y^2)dy=ay^2-2/3y^3$ .

He знаком c таким понятием. Если это из учебника, то приложите скан. У вас там вообще новая величина появилась- .

Представьте, что фигура получилась при поперечном сечении тела. Затем тело разрезают уже в продольном направлении, например, в верхушке. Остальную часть мысленно отбрасывают, и получается при какой-то высоте продольного сечения заштрихованная площадь. Эта площадь рассматривается как самостоятельная и в данном случае рассматривается её изменение до оси $$0x$$

. Одной из геометрических характеристик площади является как раз статический момент. Смысла нет определять его для всей фигуры относительно осей, проходящих через центр тяжести - он равен нулю. Поэтому его максимальное значение для заштрихованной площади будет тогда, когда заштрихованная площадь (площадь треугольника) совпадет c половинкой ромба. Площадь обозначается заглавной буквой $$A$$

.

qwertylol писал(а):Source of the post Потом ещё непонятно какой интеграл, если неопределённый, то где константа? A если определённый от до , то как игреки интегрирование пережили?

Интеграл определенный, т.к. $$y$$

изменяется от $$0$$

до

.

qwertylol писал(а):Source of the post
Наума писал(а):Source of the post
Затем находим зависимость размера от : из подобия треугольников.

He знаю из какого подобия, но это не верно. Точнее это верно только для квадрата, a по условию у вас ромб.

Ну вот, смотрите $\frac {B}{2(a-y)}=\frac {a}{a}=tg45$ .

qwertylol · Сообщение **qwertylol** » 18 дек 2009, 07:55

Наума писал(а):Source of the post
Интеграл определенный, т.к. изменяется от до .

Ну и как игреки интегрирование пережили, если они изменяются?

Наума писал(а):Source of the post
Ну вот, смотрите $\frac {B}{2(a-y)}=\frac {a}{a}=tg45$ .

Возьмите произвольный ромб, не являющийся квадратом и убедитесь, что это неверно.
Кстати у Фихтенгольца статический момент вообще находится отдельно по каждой оси. Причём ни по какой оси он не совпадает c вашим.

Наума · Сообщение **Наума** » 18 дек 2009, 15:36

Извиняюсь, рисунок неточно изобразила и поэтому не получалось, я уже исправила его.
Функция получилась такая $\tau (y) =\frac {Q(a^2+ay-2y^2)}{6J}$ . Она имеет максимум $max\tau (a/4) =\frac {3Qa^2}{16J}$ , который совпадает c рисунком. Выведенная формула является касательным напряжением, распределенным по высоте сечения балки при плоском поперечном изгибе. B сопротивлении материалов один сплошной матан. Спасибо за внимание .

yourdomain.com