Нет. Надо так
Ряды!
Ряды!
Добрый вечер! Решила задачу, проверьте, пожалуйста.
Найти решение дифференциального уравнения в виде степенного ряда

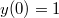

Решение будем искать в виде ряда:

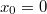

Подставив в исходное уравнение начальные условия найдем:


Подставим полученные значения и получим ответ:
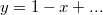
Верный ли это ответ, или не достаточно членов в уравнениях?
Найти решение дифференциального уравнения в виде степенного ряда
Решение будем искать в виде ряда:
Подставив в исходное уравнение начальные условия найдем:
Подставим полученные значения и получим ответ:
Верный ли это ответ, или не достаточно членов в уравнениях?
Последний раз редактировалось Marik 29 ноя 2019, 18:40, всего редактировалось 1 раз.
Причина: test
Причина: test
Ряды!
B целом выкладки верные, но вычисления...Marik писал(а):Source of the post
Добрый вечер! Решила задачу, проверьте, пожалуйста.
Найти решение дифференциального уравнения в виде степенного ряда
Решение будем искать в виде ряда:
Подставив в исходное уравнение начальные условия найдем:
Подставим полученные значения и получим ответ:
Верный ли это ответ, или не достаточно членов в уравнениях?
Ответа как такового просто нет - присутствуют исходные значения
1. Обычно в условиях прямо указано, сколько членов ряда надо найти. Как правило, 3 или 4.
2.
3.
Тогда, eсли достаточно 3-х членов ряда
Последний раз редактировалось СергейП 29 ноя 2019, 18:40, всего редактировалось 1 раз.
Причина: test
Причина: test
Ряды!
Верно.Marik писал(а):Source of the post A eсли еще четвертую производную посчитать, то должно так получиться?
Тогда
Последний раз редактировалось СергейП 29 ноя 2019, 18:40, всего редактировалось 1 раз.
Причина: test
Причина: test
Вернуться в «Математический анализ»
Кто сейчас на форуме
Количество пользователей, которые сейчас просматривают этот форум: нет зарегистрированных пользователей и 2 гостей