yourdomain.com

Добрый день!
Вопрос: если попытка описать совершенный кубоид приводит к однородной системе из восьми линейных уравнений, определитель которой в общем виде не равен нулю, означает ли это, что возможны только нулевые решения?

Андрей А. писал(а):Source of the post
если попытка описать совершенный кубоид приводит к однородной системе из восьми линейных уравнений

Линейных?!!! Это означает, что Ваша система не имеет к описанию ни малейшего касательства.

[quote=]Не верю[/quote]

Быстро не получится, но я выложу. А Вы укажите на ошибку. Идет?

Решим сначала в целых числах уравнение $$X^2=Y^2+Z^2+T^2$$

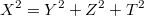
, где

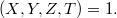
Если

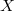
четно, то квадраты в правой части не могут быть все нечетны, и наоборот, если $$X$$

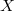
нечетно, то в правой части есть хотя бы один нечетный квадрат. Иными словами, в правой части имеется квадрат той же четности, что и $$X$$

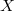
. Положим это $$Y$$

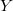
, и находятся $$P,Q$$

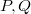
такие, что $P+Q=X;\ P-Q=Y$ .
Тогда $$X^2-Y^2=(P+Q)^2-(P-Q)^2=4PQ=Z^2+T^2.$$

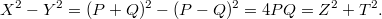
Отсюда видно, что $$Z,T$$

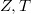
- четные, кроме того $$P,Q$$

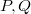
делят

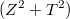
и являются числами того же вида. То есть находятся $$a,b,c,d$$

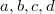
, для которых выполняется $a^2+b^2=P;\ c^2+d^2=Q;\ 2ac+2bd=Z;\ 2ad-2bc=T.$ Отсюда $X=a^2+b^2+c^2+d^2;\ Y=a^2+b^2-c^2-d^2.$ Тут есть нюансы, но в любом случае тождество $$(a^2+b^2+c^2+d^2)^2=(a^2+b^2-c^2-d^2)^2+(2ac+2bd)^2+(2ad-2bc)^2$$

$$(a^2+b^2+c^2+d^2)^2=(a^2+b^2-c^2-d^2)^2+(2ac+2bd)^2+(2ad-2bc)^2$$

полностью описывает пропорциональные решения с коэффициентом $$2$$

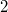
или

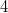
(в случае нечетных $$a,b,c,d$$

).

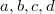
Возьмем теперь кубоид с соответствующими ребрами и пространственной диаганалью. Запишем выражения для квадратов лицевых диаганалей:
$$(a^2+b^2+c^2+d^2)^2-(a^2+b^2-c^2-d^2)^2=4(a^2+b^2)(c^2+d^2)$$

$$(a^2+b^2+c^2+d^2)^2-(a^2+b^2-c^2-d^2)^2=4(a^2+b^2)(c^2+d^2)$$

$$(a^2+b^2+c^2+d^2)^2-(2ac+2bd)^2=((a+c)^2+(b+d)^2)((a-c)^2+(b-d)^2)$$

$$(a^2+b^2+c^2+d^2)^2-(2ad-2bc)^2=((a+d)^2+(b-c)^2)((a-d)^2+(b+c)^2)$$

Для решения задачи о совершенном кубоиде достаточно, чтобы во всех трех строках оказались целые квадраты. Для выражения $$(a^2+b^2)(c^2+d^2)$$

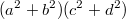
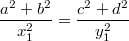
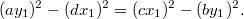
такое утверждение равносильно следующему: существуют целые $x_1;y_1\neq 0$ такие, что $\frac{a^2+b^2}{x_1^2}=\frac{c^2+d^2}{y_1^2}$ . Перепишем это как $$(ay_1)^2-(dx_1)^2=(cx_1)^2-(by_1)^2.$$

$$(ay_1)^2-(dx_1)^2=(cx_1)^2-(by_1)^2.$$

Решения такого уравнения известны: $ay_1=\frac{p_1z_1+q_1t_1}{2};\ dx_1=\frac{p_1z_1-q_1t_1}{2};\ cx_1=\frac{p_1t_1+q_1z_1}{2};\ by_1=\frac{p_1t_1-q_1z_1}{2}.$ Записываем:
$a=\frac{p_1z_1+q_1t_1}{2y_1}$
$b=\frac{p_1t_1-q_1z_1}{2y_1}$
$c=\frac{p_1t_1+q_1z_1}{2x_1}$
$d=\frac{p_1z_1-q_1t_1}{2x_1}$
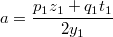
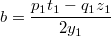
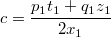
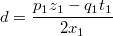
Для второй строки аналогично:
$a+c=\frac{p_2z_2+q_2t_2}{2y_2}=\frac{p_1z_1+q_1t_1}{2y_1}+\frac{p_1t_1+q_1z_1}{2x_1}$
$b+d=\frac{p_2t_2-q_2z_2}{2y_2}=\frac{p_1t_1-q_1z_1}{2y_1}+\frac{p_1z_1-q_1t_1}{2x_1}$
$a-c=\frac{p_2t_2+q_2z_2}{2x_2}=\frac{p_1z_1+q_1t_1}{2y_1}-\frac{p_1t_1+q_1z_1}{2x_1}$
$b-d=\frac{p_2z_2-q_2t_2}{2x_2}=\frac{p_1t_1-q_1z_1}{2y_1}-\frac{p_1z_1-q_1t_1}{2x_1}$
И для третьей:
$a+d=\frac{p_3z_3+q_3t_3}{2y_3}=\frac{p_1z_1+q_1t_1}{2y_1}+\frac{p_1z_1-q_1t_1}{2x_1}$
$b-c=\frac{p_3t_3-q_3z_3}{2y_3}=\frac{p_1t_1-q_1z_1}{2y_1}-\frac{p_1t_1+q_1z_1}{2x_1}$
$a-d=\frac{p_3t_3+q_3z_3}{2x_3}=\frac{p_1z_1+q_1t_1}{2y_1}-\frac{p_1z_1-q_1t_1}{2x_1}$
$b+c=\frac{p_3z_3-q_3t_3}{2x_3}=\frac{p_1t_1-q_1z_1}{2y_1}+\frac{p_1t_1+q_1z_1}{2x_1}$
Должны ли дроби быть сократимы - вопрос не главный, поскольку из рациональных решений всегда можно приготовить целые. Забывая на время о переменных $$a,b,c,d$$

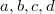
, получаем однородную систему из восьми уравнений:
$$p_1z_1x_1y_2+q_1t_1x_1y_2+p_1t_1y_1y_2+q_1z_1y_1y_2-p_2z_2y_1x_1-q_2t_2y_1x_1=0$$

$$p_1t_1x_1y_2-q_1z_1x_1y_2+p_1z_1y_1y_2-q_1t_1y_1y_2-p_2t_2y_1x_1+q_2z_2y_1x_1=0$$

$$p_1z_1x_1x_2+q_1t_1x_1x_2-p_1t_1y_1x_2-q_1z_1y_1x_2-p_2t_2y_1x_1-q_2z_2y_1x_1=0$$

$$p_1t_1x_1x_2-q_1z_1x_1x_2-p_1z_1y_1x_2+q_1t_1y_1x_2-p_2z_2y_1x_1+q_2t_2y_1x_1=0$$

$$p_1z_1x_1y_3+q_1t_1x_1y_3+p_1z_1y_1y_3-q_1t_1y_1y_3-p_3z_3y_1x_1-q_3t_3y_1x_1=0$$

$$p_1t_1x_1y_3-q_1z_1x_1y_3-p_1t_1y_1y_3-q_1z_1y_1y_3-p_3t_3y_1x_1+q_3z_3y_1x_1=0$$

$$p_1z_1x_1x_3+q_1t_1x_1x_3-p_1z_1y_1x_3+q_1t_1y_1x_3-p_3t_3y_1x_1-q_3z_3y_1x_1=0$$

$$p_1t_1x_1x_3-q_1z_1x_1x_3+p_1t_1y_1x_3+q_1z_1y_1x_3-p_3z_3y_1x_1+q_3t_3y_1x_1=0$$

Относительно переменных $$x_2,y_2,z_2,t_2,x_3,y_3,z_3,t_3$$

система линейна, и определитель системы в общем виде не равен нулю:
${\tiny \begin{pmatrix} 0 & p_1z_1x_1+q_1t_1x_1+p_1t_1y_1+q_1z_1y_1 & -p_2y_1x_1 & -q_2y_1x_1 & 0 & 0 & 0 & 0\\ 0 & p_1t_1x_1-q_1z_1x_1+p_1z_1y_1-q_1t_1y_1 & q_2y_1x_1 & -p_2y_1x_1 & 0 & 0 & 0 & 0\\ p_1z_1x_1+q_1t_1x_1-p_1t_1y_1-q_1z_1y_1 & 0 & -q_2y_1x_1 & -p_2y_1x_1 & 0 & 0 & 0 & 0\\ p_1t_1x_1-q_1z_1x_1-p_1z_1y_1+q_1t_1y_1 & 0 & -p_2y_1x_1 & q_2y_1x_1 & 0 & 0 & 0 & 0\\ 0 & 0 & 0 & 0 & 0 & p_1z_1x_1+q_1t_1x_1+p_1z_1y_1-q_1t_1y_1 & -p_3y_1x_1 & -q_3y_1x_1\\ 0 & 0 & 0 & 0 & 0 & p_1t_1x_1-q_1z_1x_1-p_1t_1y_1-q_1z_1y_1 & q_3y_1x_1 & -p_3y_1x_1\\ 0 & 0 & 0 & 0 & p_1z_1x_1+q_1t_1x_1-p_1z_1y_1+q_1t_1y_1 & 0 & -q_3y_1x_1 & -p_3y_1x_1\\ 0 & 0 & 0 & 0 & p_1t_1x_1-q_1z_1x_1+p_1t_1y_1+q_1z_1y_1 & 0 & -p_3y_1x_1 & q_3y_1x_1 \end{pmatrix}}$

Возникает мысь приравнять определитель к нулю и получить аргументы для системы с меньшим количеством уравнений, но тут я ни в чем не уверен. Отсюда и вопрос.

Андрей А. писал(а):Source of the post
Отсюда видно, что являются числами того же вида. То есть находятся , для которых выполняется $a^2+b^2=P;\ c^2+d^2=Q;\ 2ac+2bd=Z;\ 2ad-2bc=T.$

А это откуда следует?

Hottabych писал(а):Source of the post
А это откуда следует?

А ниоткуда не следует, спасибо за хороший вопрос. Размышляя в одиночку, упускаешь очевидные вещи. Полагая $Z=2Z_1;\ T=2T_1$ , получаем уравнение $$PQ=Z_1^2+T_1^2$$

, и конечно $$(a^2+b^2)(c^2+d^2)=(ac+bd)^2+(ad-bc)^2$$

не является полным решением. Тему это не перечеркивает, просто ограничивает круг решений.
Полное решение вероятно можно получить из восьми переменных, сделав подстановку $P\rightarrow (a_1c_1+b_1d_1)^2+(a_1d_1-b_1c_1)^2;\ Q\rightarrow (a_2c_2+b_2d_2)^2+(a_2d_2-b_2c_2)^2$ и довольно длинные выражения для $$Z_1;T_1$$

. Если это придется ко двору, выложу конечно, но кажется легче исходить из решений Острика-Цфасмана (в конце книги), опуская рациональный коэффициент. Тогда квадраты лицевых диагоналей такие получаются:
$$4(ln)^2[(kn)^2+(lm)^2]$$

$$[(kn)^2+(l(m+n))^2][(kn)^2+(l(m-n))^2]$$

$$[(lm)^2+(n(k+l))^2][(lm)^2+(n(k-l))^2]$$

Тут аналогичная система может еще проще оказаться.

yourdomain.com

Пифагоров кирпич

Пифагоров кирпич

Пифагоров кирпич

Пифагоров кирпич

Пифагоров кирпич

Пифагоров кирпич

Пифагоров кирпич