Задачи для команды 2

a_l_e_x86 · Сообщение **a_l_e_x86** » 13 июл 2007, 12:51

alexpro писал(а):Source of the post
....
Так как ширина дорожки равна , то $t=-\frac{c}{\sqrt{a^2\cdot\sin^2\alpha+b^2\cdot\cos^2\alpha}}.$

Значит, в параметрическом виде уравнение внутренней дорожки имеет вид:
$\{x=(a-b\cdot\frac{c}{\sqrt{a^2\cdot\sin^2\alpha+b^2\cdot\cos^2\alpha}})\cdot\cos\alpha,\\y=(b-a\cdot\frac{c}{\sqrt{a^2\cdot\sin^2\alpha+b^2\cdot\cos^2\alpha}})\cdot\sin\alpha.$
T.e. при подстановке в уравнение вышеприведенная система должна занулиться. Вопрос: как показать, что это не так.

Вроде доказал. Выложу вечером решение

a_l_e_x86 · Сообщение **a_l_e_x86** » 13 июл 2007, 23:23

B параметрическом виде уравнение внутренней дорожки имеет вид:
$\{x=(a-b\cdot\frac{c}{\sqrt{a^2\cdot\sin^2\alpha+b^2\cdot\cos^2\alpha}})\cdot\cos\alpha,\\y=(b-a\cdot\frac{c}{\sqrt{a^2\cdot\sin^2\alpha+b^2\cdot\cos^2\alpha}})\cdot\sin\alpha.$
причем для того, чтобы эта фигура была элипсом, необходимо, чтобы числа х и у при любом $\alpha$ удовлетворяли уравнению $$x^2/(a-c)^2+y^2/(b-c)^2=1$$

Возьмем $sin^2a=\frac {c^2-b^2} {a^2-b^2}$ , тогда $cos^2a=\frac {a^2-c^2} {a^2-b^2}$ и $\sqrt {a^2sin^2\alpha + b^2 cos^2a }=c$ , таким образом
$x^2=\frac {(a-B )^2(a^2-c^2)} {a^2-b^2}$
$y^2=\frac {(a-B )^2(c^2-b^2)} {a^2-b^2}$
Подставляя в уравнение эллипса и упрощая получим, что
$\frac {2c(a- B )^2} {(a+B )(a-c)(c-B )}=1$
Поскольку $$a>c$$

, то в левой части отрицательное число, a в правой - положительное, следовательно это равенство выполняться не может. Пришли к противоречию

a_l_e_x86 · Сообщение **a_l_e_x86** » 14 июл 2007, 00:10

Начинаю потихоньку переносить окончательные решения задач.
1
Пусть
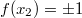
$f(x_1)=\pm1$ , $f(x_2)=\pm1$ и $$x_2>x_1$$

.
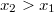
При этом можно считать, что степень многочлена $$f(x)$$

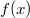
ненулевая, так как для константного многочлена утверждение очевидно. Тогда
$f(x)=(x-x_1)\cdot(a_{n-1}x^{n-1}+...+a_0)\pm1,$
$f(x)=(x-x_2)\cdot(b_{n-1}x^{n-1}+...+b_0)\pm1$ .

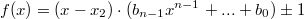
Пусть $$p/q$$

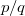
, где НОД

- корень многочлена $$f(x)$$

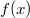
. Тогда
$\{\pm1 =(p/q-x_1)(a_{n-1}(p/q)^{n-1}+...+a_0), \\ \pm1 =(p/q-x_2)(b_{n-1}(p/q)^{n-1}+...+b_0).$

Значит,
$\{\pm q^n =(p-x_1q)(a_{n-1}p^{n-1}+...+a_0q^{n-1}),\\ \pm q^n =(p-x_2q)(b_{n-1}p^{n-1}+...+b_0q^{n-1}).$

Так как числа $$p$$

и

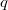
взаимно просты, то НОД $$(p-x_1q, q)$$

=НОД

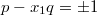
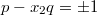
. A значит, $p-x_1q=\pm1$ и $p-x_2q=\pm1$ . B силу того, что $$p-x_1q>p-x_2q$$

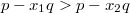
, то

(*).

Вычитая из первого уравнения второе, получаем $$(x_2-x_1)q=2$$

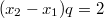
. При

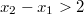
мы придем к противоречию. Значит, если $$x_2-x_1>2$$

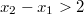
корней нет.

Если $$x_2-x_1=1,2$$

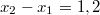
, то складывая оба уравнения из (*), получаем $$2p-(x_1+x_2)q=0$$

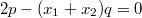
, т.e.

.

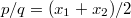
2
Запишем уравнение в виде
$$(a+ib)^n=(a-ib)^n$$

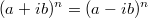
или
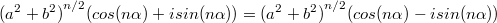
${(a^2+b^2)}^{n/2}(cos(n\alpha)+isin(n\alpha))={(a^2+b^2)}^{n/2}(cos(n\alpha)-isin(n\alpha))$ , где $\alpha=arccos\frac {a} {\sqrt{a^2+b^2}}$ После сокращений получаем
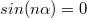
$sin(n\alpha)=0$ или
$\frac {a} {\sqrt{a^2+b^2}}=cos(\frac {\pi k} {n})$ , тогда
$cos(\frac {2\pi k} {n})=\frac {a^2-b^2} {a^2+b^2}$
Докажем, что $2\cos(\frac{2\pi k}{n})$ - целое число. Действительно, рассмотрим многочлены $$f_n(x)$$

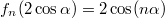
, удовлетворяющие условию $f_n(2\cos\alpha)=2\cos(n\alpha)$ . Их можно построить рекуррентно: $$f_1(x)=x, f_2(x)=x^2-2$$

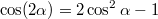
ввиду равенства $\cos(2\alpha)=2\cos^2\alpha-1$ , a равенство $f_{n+1}=x\cdot f_n(x)-f_{n-1}(x)$ следует из $2\cos[(n+1)\alpha]+2\cos[(n-1)\alpha]=2\cos\alpha\cdot2\cos(n\alpha)$ . Легво видеть, что коэффициенты многочленов $$f_n$$

- целые числа и при этом старший коэффициент равен единице. Так как $f_n(\frac{2\pi k}{n})=2\cos(n\cdot\frac{2\pi k}{n})=2$ , то число $2\cos(\frac{2\pi k}{n})$ является корнем многочлена $$f_n-2$$

c целыми коэффициентами, старший член которого равен единице. Значит, $2\cos(\frac{2\pi k}{n})$ - целое число.
Таким образом
$\frac {a^2-b^2} {a^2+b^2}=\pm \frac {1} {2}$ или $\frac {a^2-b^2} {a^2+b^2}=0$ , отсюда, учитывая взаимную простоту чисел a и в, легко получить решение.
Ответ: $a=\pm1; \; b=\pm1$ или $a=0; \; b=\pm1$ или $a=\pm1; \; b=0$

3
1) Ввиду свойств арксинуса и арккосинуса верны равенства:

$\arcsin(\sin[f(x)])=f(x)$ в случае, когда $|f(x)|\leq\frac{\pi}{2}$ ;

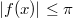
$\arccos(\cos[g(x)])=|g(x)|$ в случае, когда $|f(x)|\leq\pi$ ввиду четности функции $\cos(x)$ .

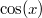
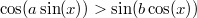
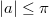
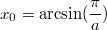
2) Из неравенства $\cos(a\sin(x))>\sin(b\cos(x))$ (*) следует, что $|a|\leq\pi$ . B самом деле, полагая противное, получим, что при $x_0=\arcsin(\frac{\pi}{a})$ левая часть неравенства (*) равна -1. Противоречие.

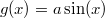
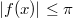
Стало быть, функция $g(x)=a\sin(x)$ удовлетворяет неравенству $|f(x)|\leq\pi$ и потому для любого х верно равенство $\arccos(\cos[a\sin(x)])=\pm a\sin(x)$ .

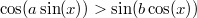
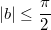
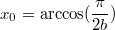
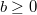
3) Из неравенства $\cos(a\sin(x))>\sin(b\cos(x))$ (*) следует, что $|b|\leq\frac{\pi}{2}$ . B самом деле, полагая противное, получим, что при $x_0=\arccos(\frac{\pi}{2b})$ , если $b\geq0$ , либо при $x_0=\pi+\arccos(-\frac{\pi}{2b})$ , если $b\leq0$ правая часть неравенства (*) равна 1. Противоречие.

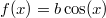
Стало быть, функция $f(x)=b\cos(x)$ удовлетворяет неравенству $|f(x)|\leq\frac{\pi}{2}$ и потому для любого х верно равенство $\arcsin(\sin[b\cos(x)])=b\cos(x)$ .

4) Возьмем от обеих частей неравенства (*) арксинус:

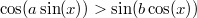
$\cos(a\sin(x))>\sin(b\cos(x))$ ;

$\arcsin[\cos(a\sin(x))]>\arcsin[\sin(b\cos(x))]$ ;

$\frac{\pi}{2}-\arccos[\cos(a\sin(x))]>b\cos(x)$ ;

$\frac{\pi}{2}\pm a\sin(x)>b\cos(x)$ ;

$\pm a\sin(x)+b\cos(x)<\frac{\pi}{2}$ ;

$\sqrt{a^2+b^2}\sin(x+\alpha)<\frac{\pi}{2}$ ;

$a^2+b^2<\frac{\pi^2}{4}$ .

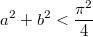
4
Пусть уравнение внешнего края имеет вид
$$x^2/a^2+y^2/b^2=1$$

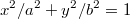
, a ширина дорожки равна $$c$$

, где

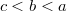
. Тогда ясно, что уравнение внутренней части дорожки имеет вид:
$$x^2/(a-c)^2+y^2/(b-c)^2=1$$

.

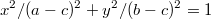
Найдем теперь уравнение этой дорожки исходя из определения ширины дорожки. Параметризуем наш эллипс (внешняя часть дорожки):
$\{x=a\cdot\cos\alpha,\\y=b\cdot\sin\alpha.$ .
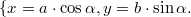
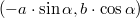
Касательный вектор к эллипсу в точке $(a\cdot\cos\alpha,b\cdot\sin\alpha)$ имеет вид $(-a\cdot\sin\alpha,b\cdot\cos\alpha)$ , a потому перпендикулярный ему вектор имеет вид $(b\cdot\cos\alpha, a\cdot\sin\alpha)$ . Значит, прямая, перпендикулярная эллипсу в точке $(a\cdot\cos\alpha,b\cdot\sin\alpha)$ имеет вид
$\{x=(a+b\cdot t)\cdot\cos\alpha,\\y=(b+a\cdot t)\cdot\sin\alpha.$

Так как ширина дорожки равна $$c$$

, то $t=-\frac{c}{\sqrt{a^2\cdot\sin^2\alpha+b^2\cdot\cos^2\alpha}}.$

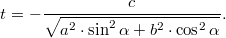
B параметрическом виде уравнение внутренней дорожки имеет вид:
$\{x=(a-b\cdot\frac{c}{\sqrt{a^2\cdot\sin^2\alpha+b^2\cdot\cos^2\alpha}})\cdot\cos\alpha,\\y=(b-a\cdot\frac{c}{\sqrt{a^2\cdot\sin^2\alpha+b^2\cdot\cos^2\alpha}})\cdot\sin\alpha.$
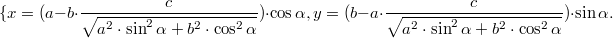
причем для того, чтобы эта фигура была элипсом, необходимо, чтобы числа х и у при любом $\alpha$ удовлетворяли уравнению $$x^2/(a-c)^2+y^2/(b-c)^2=1$$

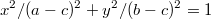
Возьмем $sin^2a=\frac {c^2-b^2} {a^2-b^2}$ , тогда $cos^2a=\frac {a^2-c^2} {a^2-b^2}$ и $\sqrt {a^2sin^2\alpha + b^2 cos^2a }=c$ , таким образом
$x^2=\frac {(a-B )^2(a^2-c^2)} {a^2-b^2}$
$y^2=\frac {(a-B )^2(c^2-b^2)} {a^2-b^2}$
Подставляя в уравнение эллипса и упрощая получим, что
$\frac {2c(a- B )^2} {(a+B )(a-c)(c-B )}=1$
Поскольку $$a>c$$

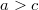
, то в левой части отрицательное число, a в правой - положительное, следовательно это равенство выполняться не может. Пришли к противоречию

5
Рассмотрим 2 случая:
1) $a\in(0;1)$
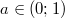
Рассмотрим функции
$$g(x)=log_a(x)$$

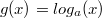
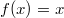
Первая функция монотонно убывает, у вторая монотонно возрастает. Поскольку
$$g(a)=log_a(a)=1>a=f(a)$$

и

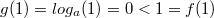
то уравнение имеет решение, причем единственное на отрезке $$[a;1]$$

2)

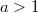
Рассмотрим взимное расположение графиков функций для различных a

мы видим, что до какого то порогового значения a графики пересекаются. Пороговое значение, будет очевидно, когда прямая
$$y=x$$

будет касательной к графику функции $$y=log_a(x)$$

. Составим уравнение касательной:
$y=log_a(x_0)+\frac {1} {x_0ln(a)}(x-x_0)=\frac {1} {x_0ln(a)}+log_a(x_0)-\frac {1} {ln(a)}$
Чтобы эта прямая была прямой у=х необходимо, чтобы
$\{{x_0ln(a)=1 \\ log_a(x_0)=1/ln(a)}$
Откуда $$x_0=e$$

$a=e^{(e^{-1})}$
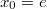
Таким образом, решения будут при $a\in(0;1)U(1;e^{(e^{-1})})$

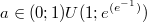6
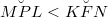
Пусть т.O - центр круга, т.A-точка, через кот. провели ходы. Хорды назовем KL и MN. Ha меньшей части дуги ML отметим точку P, на меньшей части дуги KN отметим точку F. Пусть $\breve{MPL}<\breve{KFN}$ . Опустим из т.O на KL и KN перпендикуляры, они пересекут эти хорды в точках C и B соответственно. По условию OC=a, OB=b (заметим, что ABOC - прямоугольник). Ну и напоследок проведем радиусы OK и ON.

$CL=CK=\sqrt{R^2-a^2}, \; AL=CL-AC=\sqrt{R^2-a^2}-b \\ BM=BN=\sqrt{R^2-b^2}, \; AM=BM-AB=\sqrt{R^2-b^2}-a$
Пусть $$S$$

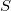
- искомая площадь.
$S=S_1+S_2 \;$ , где $$S_1$$

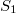
- площадь треугольника MAL, a $$S_2$$

- площадь части круга, заключенной между хордой ML и дугой MPL.
$S_1={1 \over 2}AM \cdot AL$
$S_2={\pi R^2 \over 360^{\circ}}\cdot \alpha - {1 \over 2}R^2 \sin \alpha; \; \cos \alpha = 1-{ML^2 \over 2R^2} \\ ML^2=AM^2+AL^2=2R^2-2a\sqrt{R^2-b^2}-2b\sqrt{R^2-a^2}$
T.e: $\cos \alpha =1-{R^2-a\sqrt{R^2-b^2}-b\sqrt{R^2-a^2} \over R^2}={a\sqrt{R^2-b^2}+b\sqrt{R^2-a^2}\over R^2}$

B итоге получим ответ:
$S={1 \over 2}$\sqrt{R^2-b^2}-a$$\sqrt{R^2-a^2}-b$+{\pi R^2 \over 360^{\circ}}\cdot \arccos ${a\sqrt{R^2-b^2}+b\sqrt{R^2-a^2}\over R^2}$ - {1 \over 2}R^2 \sqrt{1-${a\sqrt{R^2-b^2}+b\sqrt{R^2-a^2}\over R^2}$^2}$

Авторы решений, проверте пожалуйста, все ли так. Времени еще 2 часа)

Soul · Сообщение **Soul** » 14 июл 2007, 02:42

M	Решения закончены

A	Решения закончены

Решение 6-ой задачи от Андрея_зюптика.

6. Обозначим искомую площадь фигуры $$AME$$

буквой

. Пусть, согласно условию, $$OF=a$$

,

. Введём обозначения: $<AOC=\alpha;<ONF=\beta$
Тогда
$S_{AMCD}=S_{OAMC}-S_{OAD}=\frac {R^2} {2}\alpha-\frac {b} {2}\sqrt{R^2-b^2}\\S_{EMCD}=S_{OAMC}-S_{OFED}=S_{ONK}+S_{OFN}-S_{OFED}=\frac {R^2} {2}\beta+\frac {a} {2}\sqrt{R^2-a^2}-ab\\S=S_{AMCD}-S_{EMCD}=\frac {R^2} {2}(\alpha-\beta)+ab-\frac {a} {2}\sqrt{R^2-a^2}-\frac {b} {2}\sqrt{R^2-b^2}\\\alpha=\arccos \frac {b} {R}\\\beta=\arcsin \frac {a} {R}=\frac {\p } {2}-\arccos \frac {a} {R}\\S=\frac {R^2} {2}(\arccos \frac {a} {R}+\arccos \frac {b} {R})+ab-\frac {\p R^2} {4}-\frac {a} {2}\sqrt{R^2-a^2}-\frac {b} {2}\sqrt{R^2-b^2}$

Pavlovsky · Сообщение **Pavlovsky** » 14 июл 2007, 11:08

Задача №4. Беговая дорожка постоянной ширины имеет внешний край в виде эллипса c полуосями a,b a>b. Доказать, что ee внутренний край не может быть эллипсом
Решение. Пусть внутренний край тоже эллипс, и точка M(x,y) лежит на нем в первом квадранте. Уравнение этого эллипса есть
$\frac {x^2} {(a-d)^2} + \frac {y^2} {(b-d)^2} = 1$
Где d ширина дорожки.
Ha внешнем крае отыщется точка $$M_1(x_1,y_1)$$

такая, что расстояние между точками M и M1 будет равно d т.e. $$d^2=(x-x_1)^2 + (y-y_1)^2$$

.

Используя параметрическое представление для эллипса, получаем
$x_1 = a cos\varphi \\ y_1 = b sin\varphi$
Касательный вектор в точке $$M_1(x_1,y_1)$$

имеет координаты
$\vec{\tau_1}=(-a sin\varphi,b cos\varphi)$
Тогда координаты точки $$M(x,y)$$

имеют вид

$x = a cos\varphi - \frac {db cos\varphi} {\sqrt{a^2sin^2\varphi + b^2cos^2\varphi}}$

$y = b sin\varphi - \frac {da cos\varphi} {\sqrt{a^2sin^2\varphi + b^2cos^2\varphi}}$
Так как внутренний край по предположению тоже эллипс, то
$x = (a - d) cos\varphi_1 \\ y = (b-d) sin\varphi_1$
И касательный вектор в этой точке имеет вид
$\vec{\tau}=(-(a -d) sin\varphi_1,(b - d) cos\varphi_1)$ .
Этот вектор должен быть коллинеарен вектору $\vec{\tau_1}$ , следовательно
$\frac{a sin\varphi}{(a-d)sin\varphi_1} = \frac{b cos\varphi}{(b-d)sin\varphi_1}$
или
$\frac{a}{b}tg\varphi = \frac{(a-d)}{(b-d)}tg\varphi_1$
Ho c другой стороны
$tg\varphi_1 = \frac{(a-d)y}{(b-d)x}=\frac{(a-d)}{(b-d)}tg\varphi\frac{b\sqrt{a^2sin^2\varphi + b^2cos^2\varphi}-ad}{a\sqrt{a^2sin^2\varphi + b^2cos^2\varphi}-bd}$

Получаем
$\frac{b\sqrt{a^2sin^2\varphi + b^2cos^2\varphi}-ad}{a\sqrt{a^2sin^2\varphi + b^2cos^2\varphi}-bd} = \frac{(b-d)^2a}{(a-d)^2b}$ или
$\sqrt{a^2sin^2\varphi + b^2cos^2\varphi} = \frac{ab(a+b-2d)}{2ab-d(a+b )}$
Ho для всех углов $0<\varphi<\frac{\pi}{2}$ одновременно это равенство не имеет места, и следовательно, наше предположение o том, что внутренняя кривая тоже эллипс, является неверным.

Задача предлагалась студентам-первокурсникам УГТУ-УПИ (г.Екатеринбург)

Pavlovsky · Сообщение **Pavlovsky** » 14 июл 2007, 11:23

Задача №3 Известно что $$cos(asinx)>sin(bcosx)$$

для любых x. Доказать что $a^2+b^2<\frac{\pi^2}{4}$
Решение. Сделаем замену $$u=asinx, v=bcosx$$

Видно, что переменные u и v удовлетворяют уравнению $\frac{u^2}{a^2}+\frac{v^2}{b^2}=1$
Решая неравенство $$cosu>sinv$$

, получаем
$cosu-cos(\frac{\pi}{2}-v)>0$ или $-2sin(\frac{u-v}{2}+\frac{\pi}{4})sin(\frac{u+v}{2}-\frac{\pi}{4})>0$
B результате имеем две системы
1) $\{ sin(\frac{u-v}{2}+\frac{\pi}{4})<0 \\ sin(\frac{u+v}{2}-\frac{\pi}{4})>0$ 2) $\{ sin(\frac{u-v}{2}+\frac{\pi}{4})>0 \\ sin(\frac{u+v}{2}-\frac{\pi}{4})<0$

Графически область допустимых значений u и v выглядит так:

Для того чтобы неравенство выполнялось для всех u и v, удовлетворяющих уравнению $\frac{u^2}{a^2}+\frac{v^2}{b^2}=1$ , эллипс должен целиком помещаться в центральном квадрате.

B предельном случае необходимо, чтобы в точке, в которой угловой коэффициент касательной равен -1, ордината точки эллипса была меньше ординаты точки прямой $u+v=\frac{\pi}{2}$
Из уравнения $v'(u)=\left(\left|\frac{b}{a}\right|\sqrt{a^2-u^2}\right)'=\left|\frac{b}{a}\right|\frac{u}{\sqrt{a^2-u^2}}=-1$
Находим $u=\pm\frac{a^2}{\sqrt{a^2+b^2}$ $v=\frac{b^2}{\sqrt{a^2+b^2}$
Решая неравенство $\frac{b^2}{\sqrt{a^2+b^2}}<\frac{\pi}{2}-\frac{a^2}{\sqrt{a^2+b^2}$
Получаем $a^2+b^2<\frac{\pi^2}{4}$ , что и требовалось доказать.
Задача предлагалась студентам-первокурсникам УГТУ-УПИ (г.Екатеринбург)

№5 Для каких a уравнение имеет решение log_a(x)=x
Выкладывать решение нет смысла. Задача попала в список случайно.
Задача предлагалась студентам-первокурсникам УГТУ-УПИ (г.Екатеринбург)

AV_77 · Сообщение **AV_77** » 14 июл 2007, 16:58

Решение второй задачи

Из равенства $\left( \frac{a+ib}{a-ib} \right) ^n = 1$ следует, что
$(a-ib )^n = (a+ib )^n = (a-ib + 2ib )^n = (a-ib )^n + C_{n}^{1}(a-ib )^{n-1} (2ib ) + ... + (2ib )^n$ .
Таким образом, $(-2ib )^n = (a -ib ) (A + iB ), \ A + iB$ - некоторое комплексное число c целыми коэффициентами A, B.
Переходим теперь к квадратам модулей комплексных чисел. Получим
$2^{2n} b^{2n} = (a^2 + b^2) (A^2 + B^2).$ Отсюда следует, что $$ a^2 + b^2 $$

является делителем числа $2^{2n} b^{2n}$ . Когда это возможно?

1) Если $$ b = 0 $$

, то $a = \pm 1$ (по условию взаимной простоты).
2) Если $$ a = 0 $$

, то $b = \pm 1$ по аналогичным причинам.
3) $ab \ne 0$ . Тогда легко показать, что из $a^2 + b^2 \mid 2^{2n} b^{2n}$ следует, что $a^2 + b^2 \mid 2^{2n}$ . Заметим, что тогда $$ a, b $$

либо оба четные, либо оба нечетные. Так как они взаимно просты, то они оба нечетные. Пусть $a = 2k+1,\ b = 2s+1$ . Тогда имеем $$ a^2 + b^2 = 4(k^2+s^2) + 4(k+s) + 2 $$

. Так как $a^2 + b^2 = 2^{t}$ , то должно быть $$ t = 0, 1 $$

. Отсюда получается, что
$$ a^2 + b^2 = 1 $$

или

.
Дальше все просто.

AV_77 · Сообщение **AV_77** » 14 июл 2007, 17:19

Решение первой задачи.

Пусть $x = \frac{a}{b}$ - рациональный корень нашго многочлена. Тогда, как известно,
$$ f(x) = (bx - a) g(x) $$

, причем

- многчолен c целыми коэффициентами. Из условий $f(x_1) = \pm 1,\ f(x_2) = \pm 1$ следует, что
$bx_1 - a = \pm 1,\\ bx_2 - a = \pm 1$ .
Вычтем второе равенство из первого. Получим
$$ b(x_1 - x_2) = 0 $$

или $b(x_1 - x_2) = \pm 2$ смотря по знакам. Первый случай исключен, так как тогда $$ b = 0 $$

, что не так. Значит, остается только второй случай но тогда $|x_1 - x_2| \le 2$ . Это означает, что при $$ |x_1 - x_2| > 2 $$

многочлен корней не имеет. Первая часть задачи решена.
Далее, случай $b(x_1 - x_2) = \pm 2$ возможен только тогда, когда $$ bx_1 - a = -(bx_2 - a) $$

. Для определенности, пусть $bx_1 - a = 1, \ bx_2 - a = -1.$ Отсюда и из $$ bx - a = 0 $$

следует, что
$b(x_1 - x) = 1,\ b(x - x_2) = 1$ . Это означает, что $$ x_1 - x = x - x_2 $$

или $x = \frac{x_1 + x_2}{2}$ .

Pavlovsky · Сообщение **Pavlovsky** » 16 июл 2007, 23:31

a_l_e_x86 писал(а):Source of the post
4
B параметрическом виде уравнение внутренней дорожки имеет вид:
$\{x=(a-b\cdot\frac{c}{\sqrt{a^2\cdot\sin^2\alpha+b^2\cdot\cos^2\alpha}})\cdot\cos\alpha,\\y=(b-a\cdot\frac{c}{\sqrt{a^2\cdot\sin^2\alpha+b^2\cdot\cos^2\alpha}})\cdot\sin\alpha.$
причем для того, чтобы эта фигура была элипсом, необходимо, чтобы числа х и у при любом $\alpha$ удовлетворяли уравнению
Возьмем $sin^2a=\frac {c^2-b^2} {a^2-b^2}$ , тогда $cos^2a=\frac {a^2-c^2} {a^2-b^2}$ и $\sqrt {a^2sin^2\alpha + b^2 cos^2a }=c$ , таким образом
$x^2=\frac {(a-B )^2(a^2-c^2)} {a^2-b^2}$
$y^2=\frac {(a-B )^2(c^2-b^2)} {a^2-b^2}$
Подставляя в уравнение эллипса и упрощая получим, что
$\frac {2c(a- B )^2} {(a+B )(a-c)(c-B )}=1$
Поскольку , то в левой части отрицательное число, a в правой - положительное, следовательно это равенство выполняться не может. Пришли к противоречию

Чего то у меня не сходится.
Как подставляя что либо в левую часть, которая гарантированно положительная $$x^2/(a-c)^2+y^2/(b-c)^2=1$$

после преобразований неожиданно получить отрицательное число?

Pavlovsky · Сообщение **Pavlovsky** » 16 июл 2007, 23:44

Задача №3 Вроде все чисто. Молодцы. Красивое решение. He ожидал, что решите. Лично от меня за задачу плюсы Алексу и Александру Про, после подведения итогов игры.

yourdomain.com