yourdomain.com

помогите свести к эйлерову интегралу
хотя бы подскажите замену)))

$\int_{0}^{1}{\sqrt{\frac {1-x} {x}}*\frac {dx} {(x+2)^2}}$

laplas писал(а):Source of the post
помогите свести к эйлерову интегралу
хотя бы подскажите замену)))

$\int_{0}^{1}{\sqrt{\frac {1-x} {x}}*\frac {dx} {(x+2)^2}}$

A вы уверены, что это возможно? Тем более, что тут и в элементарных всё берётся.

Наверное имеются в виду подстановки Эйлера.

в задачнике написано "используя интегралы эйлера, вычислить интеграл")) видимо имеется ввиду бета- и гамма-функции)))

я попробовал так:
замену сделал
$t=\frac {1-x} {x+2}$
$x=\frac {1-2t} {t+1}$

$dx=-\frac {(x+2)^2} {3}*dt$
отсюда имеем

$-\frac {1} {3}*\int_{0}^{1}{\sqrt{(\frac {3*t} {1-2*t})}dt}$
дальше я заменил 2*t на u.. вроде пришел к бета функции, но c ответом не сходится((
помогите плиз

laplas писал(а):Source of the post отсюда имеем

Пределы правильно пересчитали?

Ну тогда $\frac{\operatorname{B}$\frac32,\frac12$}{2\sqrt6}$ .

a куда минус перед интегралом девается??? я не пойму((((у меня отрицательный ответ получается..a в учебнике положительный

laplas писал(а):Source of the post
a куда минус перед интегралом девается??? я не пойму((((у меня отрицательный ответ получается..a в учебнике положительный

Вам уже сказали, что надо пересчитать пределы интегрирования. Получится $-\frac{1}{\sqrt{3}}\int_{1/2}^0 \sqrt{\frac{t}{1-2t}}\operatorname{d}t=\frac{1}{\sqrt{3}}\int_{0}^{1/2} \sqrt{\frac{t}{1-2t}}\operatorname{d}t$
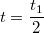
Теперь замена $t=\frac{t_1}2$ и получается интеграл Эйлера первого рода в чистом виде.

огромное спасибо))))))

yourdomain.com

эйлеровы интегралы

эйлеровы интегралы

эйлеровы интегралы

эйлеровы интегралы

эйлеровы интегралы

эйлеровы интегралы

эйлеровы интегралы

эйлеровы интегралы

эйлеровы интегралы

эйлеровы интегралы

эйлеровы интегралы