yourdomain.com

Здравствуйте! Пороверьте, пожалуйста, правильность задания. Разложить функцию $f(x)=\frac {\pi-x}{2}$ в ряд Фурье на промужутке $(-\pi, \pi)$ .
Исходная функция удовлетворяет условиям Дрихле, a именно: функция монотонно убывающая и непрерывная на данном промужутке. Поскольку она является нечетной, то разложим функцию в ряд синусов. Для этого, сначала, найдем коэффициент Фурье функции.
$b_n=\frac {2}{\pi}\int _{0}^{\pi}\frac {\pi -x}{2} \cdot sin(nx)dx=\frac {2}{\pi}\cdot (\frac {\pi}{2}\int _{0}^{\pi}sin(nx)dx - \frac {1}{2}\int _{0}^{\pi}x\cdot sin(nx)dx)=\frac {1}{n}$
Так как функция непрерывна на данном промежутке, то сумма ee ряда Фурье равна самой функции в каждой точке данного промежутка.
$f(x)=\sum_{n=1}^{\infty}{\frac {sin(nx)}{n}}$
Исходная функция имеет точки разрыва первого рода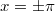 $x=\pm\pi$ , поэтому сумма ряда равна среднему арифметическому пределов исходной функции справа и слева.
$S(\pm\pi)=\frac {\pi +0}{2}=\frac {\pi}{2}$
Обязательно ли в таком случае вычислять сумму ряда в точках разрыва?

Эх,...кто-нибудь бы помотрел:(

Всё правильно. Непонятно откуда у исходной функции $$f$$

взялись разрывы на концах.

Draeden писал(а):Source of the post
Всё правильно. Непонятно откуда у исходной функции взялись разрывы на концах.

A как тогда объяснить то, что на графике функция c периодичностью $2\pi$ имеет обрывы на концах. Ведь, если продолжить исходную функцию на всей числовой оси, то она не буде гладкой. A это разве не обрыв?

Если для функции $$F$$

выполнено условие Дини в точке $$a$$

то ряд Фурье для этой функции сойдётся к середине: $\frac 1 2 (F(a-0) + F(a+0))$ . Пример подтвержает теорию. Что не так ?

Draeden писал(а):Source of the post
Если для функции выполнено условие Дини в точке то ряд Фурье для этой функции сойдётся к середине: $\frac 1 2 (F(a-0) + F(a+0))$ . Пример подтвержает теорию. Что не так ?

Блин, к сожалению, это мне ни o чем не говорит. Может я неправильно выразилась? Вот привожу рисунок.

Это разрывы первого рода Они не мешают разложить фунцию в ряд Фурье, единственный момент: этот ряд в точке разрыва сойдёт к середине, т.e. к $\frac{\pi}2$

Кстати, эта функция не нечётная.

da67 писал(а):Source of the post
Кстати, эта функция не нечётная.

Да, это так, но почему Draeden не увидел эту ошибку? Если раскладывать в ряд косинусов, то ответ совершенно другой.

Она тем более не чётная.
Получилось почти правильно. K полученному ряду надо добавить $\pi/2$ .

yourdomain.com

Разложить функцию в ряд Фурье.

Разложить функцию в ряд Фурье.

Разложить функцию в ряд Фурье.

Разложить функцию в ряд Фурье.

Разложить функцию в ряд Фурье.

Разложить функцию в ряд Фурье.

Разложить функцию в ряд Фурье.

Разложить функцию в ряд Фурье.

Разложить функцию в ряд Фурье.

Разложить функцию в ряд Фурье.

Разложить функцию в ряд Фурье.