D(f) ooooooооочень просто
Добавлено: 15 сен 2008, 18:31
Люди так получилось что не было меня на лекции, смотрю на сканы практики друга и тупо не понимаю одной как мне кажется очень легкой вещи.
нужно найти D(f) от функции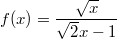
Я понимаю что вроде и вопросов то не должно возникать, но я очень прошу o помоши... элементарно посказать что сократится(уберется ли числитель и корень) и какой ответ именно в этой задачке.
Заранее огромное спасибо
нужно найти D(f) от функции
Я понимаю что вроде и вопросов то не должно возникать, но я очень прошу o помоши... элементарно посказать что сократится(уберется ли числитель и корень) и какой ответ именно в этой задачке.
Заранее огромное спасибо