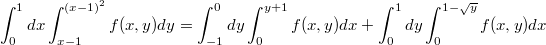Страница 5 из 17
Область, заданная неравенствами
Добавлено: 07 мар 2010, 13:53
jarik
По
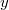
границы наоборот

A второй переход верно...
Область, заданная неравенствами
Добавлено: 07 мар 2010, 14:35
Ногин Антон
Спасибо!
Область, заданная неравенствами
Добавлено: 08 мар 2010, 08:47
Ногин Антон
Гляньте ещё такую:
Область:

;

;

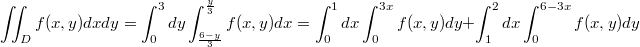
Область, заданная неравенствами
Добавлено: 08 мар 2010, 08:59
СергейП
Область, заданная неравенствами
Добавлено: 08 мар 2010, 09:05
jarik
A не наоборот

Область, заданная неравенствами
Добавлено: 08 мар 2010, 09:10
СергейП
Точно, надо наоборот.
Поспешил,
Область, заданная неравенствами
Добавлено: 08 мар 2010, 12:29
Ногин Антон
Немножко другая задача:
Нужно изменить порядок интегрирования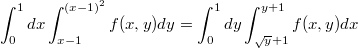
Странно как-то получилось - обычно в таких задачах получается сумма интегралов(eсли задан один).
Область, заданная неравенствами
Добавлено: 08 мар 2010, 12:35
jarik
Там и должно два получится, там где

Там где


Область, заданная неравенствами
Добавлено: 08 мар 2010, 12:46
Ногин Антон
Точно, не ту область взял. Спасибо, сейчас переделаю!
Область, заданная неравенствами
Добавлено: 08 мар 2010, 13:07
Ногин Антон
Получилось так: