yourdomain.com

Геометрия масс.
Определения и предварительные соглашения.

Предположим, что точки имеют массу, т.е. каждой точке сопоставлено не отрицательное действительное число. Точки упорядочены по массе в порядке возрастания масс. Обозначаются точки так: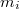 $$m_i$$

, где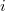

индекс, порядковый номер точки. Такие точки называются материальными точками.
Наряду с материальными, придётся рассматривать ещё геометрические точки, как точки пересечения линий, проходящих через материальные точки.

Пара упорядоченных точек задаёт вектор, т.е. направленный отрезок. По умолчанию (если не оговорено обратное,) вектор направлен от точки с меньшим индексом к точке с большим индексом. Обозначаются векторы буквой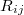 $R_{ij}$ , либо 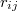$r_{ij}$ с двумя индексами. Буква $$r$$

или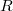

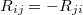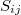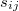говорит о том, что речь идёт о векторе. Очевидно, перестановка индексов у вектора равносильна смене направления вектора на противоположное, т.е. $R_{ij}=-R_{ji}$ Отрезки (модули векторов) будем обозначать: $S_{ij}$ или $s_{ij}$ . Порядок индексов у отрезка неважен.

Таким образом, $$n$$

точек задают цепочку $$n-1$$

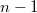векторов. Последний $$n$$

-ый вектор в цепочке векторов, замыкающий, зависим от предыдущих $$n-1$$

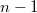векторов. Он равен сумме предыдущих векторов:
$R_{12}+R_{23}+...+R_{(n-1)n}=R_n$
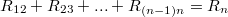
Или так:
$R_{12}+R_{23}+...-R_n=0$

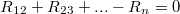
Условимся в цепочке векторов у последнего вектора менять индексы местами, т.е. для замыкающего вектора в цепочке за направление вектора по умолчанию считается направление от точки с большей массой (индексом), к точке с меньшей массой (индексом). Тогда, например, для цепочки четырёх векторов будем иметь:
$R_{12}+R_{23}+R_{34}+R_{41}=0\qquad (1)$
Такое соглашение позволяет избавиться от минуса в последнем члене и позволит впоследствии пользоваться циклической перестановкой индексов в формулах, получая при этом другие истинные формулы. В формуле (1) тоже можно циклически переставить индексы (к каждому индексу прибавить единицу, а единица, прибавленная к наибольшему индексу, заменяется единицей), равенство (1) при этом не нарушится.

Деление отрезка в данном отношении.
Центр масс двух точек.

Рассмотрим геометрическую точку $$c$$

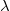, находящуюся внутри отрезка. Эта точка делит отрезок на два неравных (в общем случае) по длине меньших отрезка. Соответственно, отношения этих длин (меньших отрезков) не определено: оно может быть больше единицы или меньше единицы. Речь, по-видимому, должна идти о направленном отрезке – векторе. Под отношением $\lambda$ будем понимать отношение длин двух отрезков: отрезок от точки начала вектора, до делящей точки (делимое); и отрезок от делящей точки до точки конца вектора (делитель). Т.е.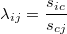 $\lambda_{ij}=\frac{s_{ic}}{s_{cj}}$
Определение: центром масс (ц.м.) двух материальных точек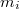 $$m_i$$

и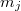

, называется геометрическая точка 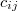$c_{ij}$ , которая делит направленный отрезок 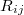$R_{ij}$ в отношении $\lambda_{ij} =\frac {m_j}{m_i}=\frac{s_{ic}}{s_{cj}}$ , При таком определении делящая точка будет находиться всегда внутри делимого направленного отрезка.

Пока достаточно, а то будет длинно.
У кого есть замечания или вопросы - прошу...

Я бы не затевал этой темы, если бы не обещал Рубен'у показать, как доказать теорему Чевы, используя понятие центра масс.

Рассмотрим треугольник масс: $m_1,\,m_2,\,m_3$ . И рассмотрим произведение отношений $\lambda_{ij}$ , в которых центры масс пар точек делят соответствующие отрезки.
$\lambda_{12}\cdot\lambda_{23}\cdot\lambda_{31}=\frac{m_2}{m_1}\cdot\frac{m_3}{m_2}\cdot\frac{m_1}{m_3}=1$
Что и требовалось.
Правда, это ещё не совсем доказательство. Предварительно нужно доказать, что система $$n$$

материальных точек имеет центр масс, причём, единственный. Чевианы проходят через ц.м. треугольника.
***Здесь тоже можно применять циклическую перестановку индексов.

Известная метода в геометрии, позволяет решать некоторый класс задач. Была книжка серии квант на эту тему)

folk писал(а):Source of the post
Известная метода в геометрии, позволяет решать некоторый класс задач. Была книжка серии квант на эту тему)

Не могли бы сказать как она называется и кто автор.
Я помню у меня была книжка "Деление отрезка в данном отношении" автор Бескин Н.М., но она потерялась.

ALEX165 писал(а):Source of the post
Эта тема позорит раздел Физика - откровенный маразм

M	Тему разделил. Разделенная тема тут.

A	Тему разделил. Разделенная тема тут.

ALEX165 писал(а):Source of the post причём кажется заразный. :angry:

Кто инфицирован? :search:

Рубен писал(а):Source of the post

ALEX165 писал(а):Source of the post причём кажется заразный. :angry:
Кто инфицирован? :search:

В той или иной мере почти все участники (кстати, психиаторы знают, что душевно больные легко вовлекают в круг своих представлений окружающих).
Понятно впрочем, в физике - на безрыбьи и рак рыба.

Разделение темы приветствую.
Придется заняться психиатрией...