Израильский суперфинал
Израильский суперфинал
https://drive.google.com/file/d/0B87lCD ... HZnBB/view
8ю я сделал, хотя факт был неожиданный.
9ю -есть простая гипотеза об ответе, посчитав определители возникающих линейных систем
10ю - мысли есть
Пояснения. 8.Выпуклость графика смотрит вниз, если бы везде была 2я производная, она была бы неотрицательна.
9.[math]
и так далее, а когда индекс превысит n, отнимать от него n
8ю я сделал, хотя факт был неожиданный.
9ю -есть простая гипотеза об ответе, посчитав определители возникающих линейных систем
10ю - мысли есть
Пояснения. 8.Выпуклость графика смотрит вниз, если бы везде была 2я производная, она была бы неотрицательна.
9.[math]
и так далее, а когда индекс превысит n, отнимать от него n
Израильский суперфинал
На счёт 10, может я условие не так понимаю...
Вот если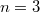 и
и 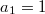 ,
, 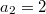 ,
, 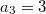 . Возьмём
. Возьмём 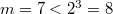 .
.
Как не выбирай, сумма элементов на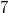 не делится...
не делится...
Вот если
Как не выбирай, сумма элементов на
Израильский суперфинал
8 довольно интуитивна - косинус в центре более отрицателен, чем по краям 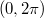 .
.
Из-за выпуклости вниз эти центральные значения имеют меньше вес, чем положительные значения по краям.
Это можно и формально расписать, если интеграл переписать как сумму интегралов по "четверть волнам" (где косинус меняется от экстремума до нуля, или обратно) а для выпуклой функции подставить неравенства.
PS: Выпуклую функцию можно сразу ограничить нулями на концах учитывая что и
и  .
.
Из-за выпуклости вниз эти центральные значения имеют меньше вес, чем положительные значения по краям.
Это можно и формально расписать, если интеграл переписать как сумму интегралов по "четверть волнам" (где косинус меняется от экстремума до нуля, или обратно) а для выпуклой функции подставить неравенства.
PS: Выпуклую функцию можно сразу ограничить нулями на концах учитывая что
Израильский суперфинал
Да, для 8 из 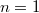 следует справедливость для остальных
следует справедливость для остальных  .
.
Это легко показать заменой переменной интегрирования.

 .
.
Это легко показать заменой переменной интегрирования.
Израильский суперфинал
Или имеется ввиду, что
Израильский суперфинал
Можно выбирать также знаки, 1+2-3=0, так как дано 6 чисел[math]. Но конечно нельзя выбрать пустое множество или становящееся таким после сокращения противоположных друг другу, для этого и сказано в условии что пару противоположных не включатьzykov писал(а):На счёт 10, может я условие не так понимаю...
Вот еслии
,
,
. Возьмём
.
Как не выбирай, сумма элементов нане делится...
Израильский суперфинал
По предварительным итогам, 10ю не решил никто, максимум наполовину.
Есть [math] комбинаций расстановки знаков в наборе [math] ,а так как [math] ,найдутся две комбинации знаков с одинаковым остатком суммы. Тогда разность сумм этих наборов делится на [math], а она имеет вид [math]- нашли набор, удвоенная сумма которого делится на [math].Это более слабое утверждение. Отсюда для [math] нечетных все доказано.
Кроме того, для [math], для которого более слабое тривиально, доказать можно все:
Тогда [math]. Если среди [math] есть четное, то выберем в [math] только его, если все нечетны, то выберем в [math] два из них.
Есть [math] комбинаций расстановки знаков в наборе [math] ,а так как [math] ,найдутся две комбинации знаков с одинаковым остатком суммы. Тогда разность сумм этих наборов делится на [math], а она имеет вид [math]- нашли набор, удвоенная сумма которого делится на [math].Это более слабое утверждение. Отсюда для [math] нечетных все доказано.
Кроме того, для [math], для которого более слабое тривиально, доказать можно все:
Тогда [math]. Если среди [math] есть четное, то выберем в [math] только его, если все нечетны, то выберем в [math] два из них.
-
peregoudov
- Сообщений: 620
- Зарегистрирован: 29 дек 2015, 13:17
Израильский суперфинал
Что выпуклая функция при ограничении на отрезок остается выпуклой, а потому из доказательства для одной волны следует доказательство для произвольного числа волн --- это понятно.
Я понял так:zykov писал(а):Source of the post Это можно и формально расписать, если интеграл переписать как сумму интегралов по "четверть волнам" (где косинус меняется от экстремума до нуля, или обратно) а для выпуклой функции подставить неравенства.
Выражение в квадратных скобка положительно в силу выпуклости (среднее по двум внутренним точкам отрезка меньше среднего по его краям).
Израильский суперфинал
peregoudov писал(а):Source of the post Выражение в квадратных скобка положительно в силу выпуклости
Да.
Израильский суперфинал
Ian писал(а):Source of the post Отсюда для m нечетных все доказано.
Кроме того, для m=2, для которого более слабое тривиально
Осталось для чётных более двух доказать.
-
peregoudov
- Сообщений: 620
- Зарегистрирован: 29 дек 2015, 13:17
Израильский суперфинал
Так вроде среди  остатков от деления на
остатков от деления на  один равен нулю? Такая комбинация подходит сама по себе, без вычитаний. А еще не обязательно, чтобы комбинации имели равные остатки. Можно взять остатки, в сумме дающие
один равен нулю? Такая комбинация подходит сама по себе, без вычитаний. А еще не обязательно, чтобы комбинации имели равные остатки. Можно взять остатки, в сумме дающие  , тогда при сложении комбинаций опять получим делимость удвоенной суммы на
, тогда при сложении комбинаций опять получим делимость удвоенной суммы на  ...
...
Израильский суперфинал
Ну это только если каждый остаток встречается не менее одного раза.
А это ещё надо доказать (если оно вообще верно).
А так просто используется Pigeonhole principle.
-
peregoudov
- Сообщений: 620
- Зарегистрирован: 29 дек 2015, 13:17
Израильский суперфинал
А вот еще соображение. Все комбинации можно получить из какой-то одной, последовательно меняя знаки отдельных  . При каждой такой замене сумма меняется на четную величину. Значит, вовсе не все остатки реализуются, а только половина.
. При каждой такой замене сумма меняется на четную величину. Значит, вовсе не все остатки реализуются, а только половина.
Израильский суперфинал
peregoudov писал(а):Source of the postВсе комбинации можно получить из какой-то одной, последовательно меняя знаки отдельных. При каждой такой замене сумма меняется на четную величину.
Можно ещё просто выбросить это
Израильский суперфинал
Ian писал(а):Source of the post Естькомбинаций расстановки знаков в наборе
, а так как
,найдутся две комбинации знаков с одинаковым остатком суммы. Тогда разность сумм этих наборов делится на
, а она имеет вид
- нашли набор, удвоенная сумма которого делится на
.
Можно сделать аналогично, но по-другому.
Тоже
Тогда найдутся два разных вектора с одинаковыми остатками от суммы по множеству.
Если взять разность этих векторов (тут коэффициенты будут
Израильский суперфинал
Действительно , 10 решена, жюри еще не публиковало.
По задаче 9. Расчеты показывают, что линейная система имеет нулевой определитель ровно при [math](степени двойки), проверено до сотни.Но доказывать удобнее не через определитель, а предъявив какое-то ненулевое решение, или противоречие, когда степень двойки. Наверное теоретически интересные какие-то ненулевые решения.
По задаче 9. Расчеты показывают, что линейная система имеет нулевой определитель ровно при [math](степени двойки), проверено до сотни.Но доказывать удобнее не через определитель, а предъявив какое-то ненулевое решение, или противоречие, когда степень двойки. Наверное теоретически интересные какие-то ненулевые решения.
-
peregoudov
- Сообщений: 620
- Зарегистрирован: 29 дек 2015, 13:17
Израильский суперфинал
А почему бы и не через определитель? Вот, например, для нечетных  нетрудно показать, что он имеет два одинаковых последних столбца.
нетрудно показать, что он имеет два одинаковых последних столбца.
Израильский суперфинал
Тогда (0;0;...0;1;-1) является подходящим набором (при n>1 !) , и это действительно так, в k-е уравнение входят переменные с номерами от k до 2k-1, и значит не может предпоследняя войти, а последняя не войти.peregoudov писал(а):А почему бы и не через определитель? Вот, например, для нечетныхнетрудно показать, что он имеет два одинаковых последних столбца.
Израильский суперфинал
Далее можно доказать, что для всех n, имеющих нечетный множитель, больший единицы - ненулевое решение системы есть.
Можно понять как оно устроено, сравнив общее решение для n=3 (0,t,-t) и для n=6 (0,t,-t,0,t,-t) - возьмем общее решение для n, равного нечетному m>1 (0,...0,t,-t) и для n, содержащего нечетный множитель m, повторим его периодически n/m раз.
В каком случае сумма компонент вектора от k-й до (2k-1)-й включительно будет равна 0? Только если суммирование разрывает либо первую встретившуюся на этом участке пару (t,-t), либо последнюю. Если начало суммирования разрывает j-ю пару, k=jm, тогда 2k-1=2jm-1 , это значит, конец суммирования разорвет [math] пару, то есть в начале k-й суммы будет непарная -t, зато в конце будет непарная t и сумма равна 0.
Обратно, если конец суммирования разорвет пару с номером i (сумма будет иметь t в конце), то последнее слагаемое будет иметь номер im-1=2k-1 (-n), тогда из четности n четно и i, i=2j, тогда начало суммирования разорвет пару j, начнется с -t
Таким образом, если n не является степенью двойки -расстановка есть.
Почему нет расстановки для n - степени двойки?
Можно понять как оно устроено, сравнив общее решение для n=3 (0,t,-t) и для n=6 (0,t,-t,0,t,-t) - возьмем общее решение для n, равного нечетному m>1 (0,...0,t,-t) и для n, содержащего нечетный множитель m, повторим его периодически n/m раз.
В каком случае сумма компонент вектора от k-й до (2k-1)-й включительно будет равна 0? Только если суммирование разрывает либо первую встретившуюся на этом участке пару (t,-t), либо последнюю. Если начало суммирования разрывает j-ю пару, k=jm, тогда 2k-1=2jm-1 , это значит, конец суммирования разорвет [math] пару, то есть в начале k-й суммы будет непарная -t, зато в конце будет непарная t и сумма равна 0.
Обратно, если конец суммирования разорвет пару с номером i (сумма будет иметь t в конце), то последнее слагаемое будет иметь номер im-1=2k-1 (-n), тогда из четности n четно и i, i=2j, тогда начало суммирования разорвет пару j, начнется с -t
Таким образом, если n не является степенью двойки -расстановка есть.
Почему нет расстановки для n - степени двойки?
Израильский суперфинал
Ian писал(а):В каком случае сумма компонент вектора от k-й до (2k-1)-й включительно будет равна 0? Только если ...
Опечатка(
...будет НЕ равна 0....
Кто сейчас на форуме
Количество пользователей, которые сейчас просматривают этот форум: нет зарегистрированных пользователей и 3 гостей