IMC-2019 1st day

[Ian]

Срочно. Мне кажется жюрийское решение Problem2 неверно, там ответ не только 2020 но и 2002 и вслед за ними еще 7 таких лет делящихся на 11. Есть даже доказательство.

imc2019-day1-solutions_copy.pdf

(125.53 KiB) Загружено 747 раз

Кто прав? Это было сегодня.

[zykov]

[math]\det \begin{pmatrix}
2 & 0 & A & R \\
R & 2 & 0 & A \\
A & R & 2 & 0 \\
0 & A & R & 2
\end{pmatrix}=-\left( R-A-2\right) \, \left( R+A+2\right) \, \left( {{R}^{2}}+(A-2)^2\right)

[zykov]

[math]\det \begin{pmatrix}2 & 0 & A & 1 \\
R & 2 & 0 & 1 \\
A & R & 2 & 1 \\
0 & A & R & 1\end{pmatrix}=-\left( R-A-2\right) \, \left( {{R}^{2}}+(A-2)^2\right)

[Ian]

Ну вот и при R=A+2 возникает серия 2002,2013,...2079 и можно проверить что там всегда б/м а не несовместность.
Сама формула циркулянта есть в общем виде https://en.wikipedia.org/wiki/Circulant_matrix
Значит жюри неправо (наших засудили...)

[Ian]

Оно признало, вот уже измененный пдф лежит для скачки

imc2019-day1-solutions (1)_copy.pdf

(131.11 KiB) Загружено 703 раз

[peregoudov]

И в чем фишка? Жюри не смогло тупо вычислить определитель четвертого порядка? (К чему там преобразования, не очень ясно.)

[Ian]

peregoudov, согласен, прога 100 циклов и ответ. Но они ж там с ручками и бумажками.
Вот 2й день условия

imc2019-day2-questions_copy.pdf

(90.02 KiB) Загружено 705 раз

6-я - это непрерывность производной по Дарбу("принимает все свои промежуточные значения"), на мехмате в 1м семестре как упражнение дают
Но пара простых задач необходимо, чтобы расставить по порядку Туркменистан например и Африку, полтысячи участников

[peregoudov]

Source of the post peregoudov, согласен, прога 100 циклов и ответ.

Да бросьте, какая прога? Определитель считается вручную тупо напрямую за 5 минут и раскладывается на множители. zykov же привел ответ. Получается отдельный корень R=0, A=2 и серия R=A+2. После чего равенство рангов главной и расширенной матриц проверяется тоже тупо руками минут за 10.

[zykov]

Я в мат. пакет (в wxmaxima) забил символьно.
Оно сразу определитель считает. И там же на множители факторизует.
1-2 минуты.

Так можно и на бумажке, как на первом курсе учили. Тоже не долго.
Ну а ошибиться любой может. Но нужно было составителю самому себя проверить в мат. пакете...

[Ian]

В работе жюри бывают случаи, когда официальное решение готовит не автор задачи и даже человек, не знакомый с ним. Я думаю это произошло из-за ограничения вопроса 21м веком,в последний момент, чтобы задача стала проще и допускала вычитания строк. В общем случае циркулянт n*n выводится временным умножением на матрицу Вандермонда из комплексных корней n-й степени из 1. http://hijos.ru/olimpiadnikam/6-matricy-i-opredeliteli/ - пункт 2.3, очень олимпиадное решение, наверное оно и было задумано, для n=4 весело выходит

[peregoudov]

Я считал определитель тупо в лоб, разложением по столбцу. Считается в две строчки, и ответ 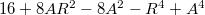. Как вообще можно было написать в ответе многочлен по 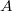третьей степени, если очевидно, что должна быть четвертая? Из квадратного трехчлена относительно 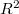выделяем полный квадрат 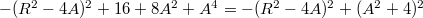, дальше тривиально раскладывается на множители.

Трдунее проверить, что ранги главной и расширенной матриц совпадают при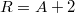 . Я считал тупо исключением Гаусса, заняло это примерно тетрадную страничку (две итерации, после чего видно, что два последних уравнения просто совпадают).

[zykov]

Source of the post Вот 2й день условия

imc2019-day2-questions_copy.pdf
(90.02 KiB) Загружено 54 раз

Ломал тут голову над задачей 9.

Найти положительные целые , такие что существуют действительные обратимые матрицы и , такие что .

У меня вроде решается, но как-то тяжеловесно и не олимпиадно. Для чётных существует, для нечётных нет.
Для очевидно не существует.
Для есть пример: и
Далее, для любого чётного можно просто заполнить главную диагональ и такими блоками и тоже получим решение.
Для нечётных вроде получается доказать, что не существует, но как-то тяжеловесно...


У кого есть какие идеи, как олимпиадно сделать?
Может я что-то из линейной алгебры упустил. Что-то про алгебру коммутаторов. Или тут можно как-то спиноры использовать (этот пример похож на спинор с нулевой мнимой частью).

Так тут слева стоит коммутатор. Но про него я знаю только что след равен нулю - мало чем помогает.
Ещё равенство можно переписать как , откуда , откуда .

[zykov]

По поводу случая 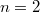, то общее решение можно получить следующим образом.
Зафиксируем матрицу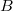 и будем искать матрицу 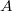. Для неё получим линейное уравнение с матрицей выраженной через 4 элемента матрицы 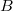. Чтобы существовало невырожденное решение для 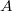, детерминант этой матрицы должен быть равен нулю.
Опуская тяжеловесные выкладки и используя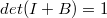 , это даёт .
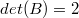Для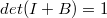 и 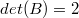матрица 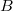должна иметь вид:


Отсюда общий вид для :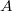


Эти 4 параметра задают все возможные варианты для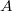 и .
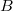( и либо , либо .)

[zykov]

По поводу того, что не существует 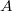и 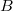для нечётных , то выходит длинно. Может уже есть какая теорма, которая тут помогает?

У меня вот так (если нигде не ошибся).
Если нечётное, то характеристический многочлен для 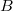- это многочлен нечётной степени с действительными коэффициентами. Значит он имеет хотя бы один действительный корень 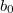. Значит для этого 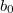матрица 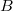имеет хотя бы один собственный вектор (как левый, так и правый). Пусть 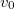- это этот левый собственный вектор, так что .
(Это известный факт - есть такая теорема.)

У нас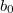 не равно нулю, т.к. 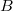обратима.
1) Умножим равенство слева на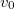 , получим , значит .
Обозначим , 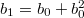и получим . Этот 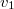не равен нулю, т.к. матрица 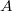обратима.
Т.е.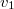 - это левый собственный вектор матрицы 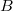с собственным значением 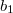. Это 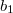не равно нулю и не равно 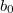. Значит 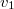линейно независим от .
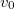2) Опять умножим равенство слева на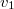 , получим .
Опять обозначим , 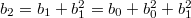и получим . Этот 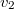не равен нулю, т.к. матрица 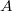обратима.
Т.е. опять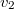 - это левый собственный вектор матрицы 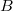с собственным значением 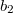. Это 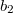не равно нулю, не равно 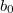и не равно 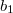. Значит 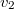линейно независим 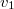от и от 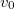. Более того, 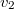не лежит в линейной оболочке 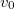и 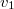. Предположим, что , тогда , значит . Но с другой стороны , значит - противоречие.
3) Аналогично, умножим равенство слева на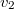 , получим .
Опять обозначим , 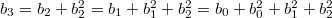и получим . Этот 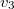не равен нулю, т.к. матрица 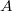обратима.
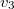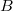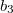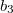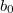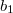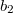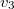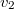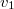Опять - это левый собственный вектор матрицы с собственным значением . Это не равно нулю, не равно , не равно и не равно . Значит линейно независим от , от и от 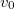. Аналогично, 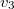не лежит в линейной оболочке 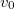, 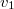и .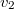
4) Тенденция ясна. Продолжим процесс для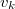 , где . ()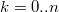
Получим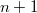 линейно независимых векторов - противоречие. Значит одновременно 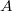и , и 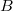не могут быть обратимыми.

[zykov]

Source of the post Опуская тяжеловесные выкладки и используя , это даёт .

Тут можно без тяжеловесных выкладок обойтись. Матрицу можно к Жордановой форме привести.
Будет два варианта: или (все не равны нулю).
обязано быть действительным. Если подставить, то сразу видно, что для второго случая решений нет.
Если и оба действительные, то тоже легко видеть, что решений нет.
Если и комплексные сопряженные друг другу, то легко определить подстановкой, что единственный вариант .
Отсюда сразу , .
Далее легко найти все действительные матрицы - либо по детерминанту и следу, либо непосредственно по собственным значениям.

[Ian]

Решение есть на сайте, и у Вас очень близко к нему
https://www.imc-math.org.uk/?year=2019&section=problems