[math], [math], [math] при [math]
Тут легко установить, какие степени ему удовлетворяют, и получить 2 линейно независимых решения [math] и [math]. Но сказано же -Лапласом, значит хотя бы ненамного сложнее, чем так. Но как?
Дифур Лапласом
-
peregoudov
- Сообщений: 620
- Зарегистрирован: 29 дек 2015, 13:17
Дифур Лапласом
Так тут, наверное, не преобразование Лапласа (которое подходит только для уравнений с постоянными коэффициентами), а метод Лапласа: поиск решения в виде интеграла по контуру. Не могу быстро найти в Гугле. Видел в "Квантовой механике" Ландау и Лифшица, одно из первых приложений. Буду дома --- смогу дать точную ссылку или даже описать идею.
-
peregoudov
- Сообщений: 620
- Зарегистрирован: 29 дек 2015, 13:17
Дифур Лапласом
Ну, в общем, это в Математических дополнениях, параграф "а". Только, оказывается, метод работает для коэффициентов, линейных по x, а тут квадратичный...
Теперь не знаю. Поскольку исходное уравнение инвариантно относительно масштабных преобразований x, заменой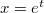 можно привести его к уравнению с постоянными коэффициентами. Но это по сути то же самое, что искать решения в виде степенных функций...
можно привести его к уравнению с постоянными коэффициентами. Но это по сути то же самое, что искать решения в виде степенных функций...
Теперь не знаю. Поскольку исходное уравнение инвариантно относительно масштабных преобразований x, заменой
Дифур Лапласом
Спасибо. Это был пример задачи к зачету, именно преобразованием Лапласа, предмет видимо называется "Доп.главы математики", там также задачи на преобр.Фурье. Мои соображения такие; если решение дифура с начальным условием в 1(в 0 нельзя) ищут преобразованием Лапласа, то его надо делать интегрированием по [math]- по тому участку, на котором нам интересно решение. Это все равно, что решать дифур со сдвинутым аргументом обычным преобразованием Лапласа.
Таким интегрированием левой части [math] надо, используя интегрирование по частям, свести это к алгебраическому уравнению относительно [math], в общем ничего невозможного,но я запутался, не хватает еще граничных условий. А казалось что преподаватель придумал хороший прием, так бы и уравнение Бесселя решалось в изображениях.
Таким интегрированием левой части [math] надо, используя интегрирование по частям, свести это к алгебраическому уравнению относительно [math], в общем ничего невозможного,но я запутался, не хватает еще граничных условий. А казалось что преподаватель придумал хороший прием, так бы и уравнение Бесселя решалось в изображениях.
-
peregoudov
- Сообщений: 620
- Зарегистрирован: 29 дек 2015, 13:17
Дифур Лапласом
Так я тоже пробовал, путаться там, вроде бы, особо негде, но получается то же самое уравнение (ну, того же типа), только теперь уже в образах.Ian писал(а):Source of the post Таким интегрированием левой части ∫∞1(x2y"+5xy′+3y)e−pxdx=0 надо, используя интегрирование по частям, свести это к алгебраическому уравнению относительно Y(p)=∫∞1y(x)e−pxdx=0, в общем ничего невозможного,но я запутался
P.S. Хотя нет, вру, понижается порядок. Вот что у меня получилось
Коэффициенты подобраны так, что после лапласа сокращается
Дифур Лапласом
Ну да, интегрированием по частям слагаемыху меня примерно то же вышлоperegoudov писал(а):
[math]
,только при доп. условии [math] которое вовсе не дано. Кто знает, как ведет себя производная решения на бесконечности. И почему-то ответ [math] отсюда совсем не очевиден
-
peregoudov
- Сообщений: 620
- Зарегистрирован: 29 дек 2015, 13:17
Дифур Лапласом
Зато понятно, как метод Лапласа из ЛЛ3 связан с преобразованием Лапласа: если сделать преобразование Лапласа уравнения с линейными коэффициентами, получается уравнение первого порядка, которое решается вариацией постоянной.
Кстати, вы уверены, что
выделяет именно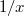 , а не
, а не 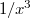 ?
?
Кстати, вы уверены, что
Ian писал(а):Source of the post y(x)=O(x−2) при x→+∞
выделяет именно
Дифур Лапласом
peregoudov писал(а):Кстати, вы уверены, чтоIan писал(а):Source of the post y(x)=O(x−2) при x→+∞
выделяет именно, а не
?
Конечно, наоборот, написал не подумав. Правильное решение дифура [math],изображение Y этой функции и должно получиться
Кто сейчас на форуме
Количество пользователей, которые сейчас просматривают этот форум: нет зарегистрированных пользователей и 3 гостей