Простые с виду вопросы про L2(0,1)
Простые с виду вопросы про L2(0,1)
1.Найти норму оператора в [math]
[math]
Тут я подобрал функцию [math], но доказать, что максимум отношения норм на ней. не могу
2. Найти функцию из [math] ,ортогональную [math] (то есть всем многочленам,обращающимся в 0 в нуле)
Тут вообще неэлементарная должна быть. Но какая?
[math]
Тут я подобрал функцию [math], но доказать, что максимум отношения норм на ней. не могу
2. Найти функцию из [math] ,ортогональную [math] (то есть всем многочленам,обращающимся в 0 в нуле)
Тут вообще неэлементарная должна быть. Но какая?
Простые с виду вопросы про L2(0,1)
Ian писал(а):Source of the post Найти функцию
Нулевая будет ортогональной.
Простые с виду вопросы про L2(0,1)
Задача 2. Ну я кажется понял в чем прикол. Если мы ортогонализацией системы [math] строим ортогональный базис Лежандра, эта система будет полной. Что, казалось бы, подсказывает, что система ортогональных полиномов, получающаяся из [math] ,будет неполной, мы же убрали одну функцию. Но с другой стороны, есть и такое стандартное рассуждение.
1.Множество непрерывных функций плотно (все в норме [math]) в [math], достаточно взять частичные суммы ряда Фурье.
2.Множество [math] непр. функций, обращающихся в 0 в нуле, плотно во множестве непрерывных функций, достаточно исправить график каждой на малом отрезке [math] .
3.Множество многочленов плотно в указанном множестве [math] непрерывных функций в равномерной норме, по Теореме Вейерштрасса. Тогда если [math] и [math] то [math] и [math], значит, нашелся и приближающий многочлен со значением 0 в нуле [math] Раз он приближает в равномерной норме, то и в норме [math]
Отсюда, многочлены с нулевым свободным членом плотны в [math] , только нулевая f может быть
1.Множество непрерывных функций плотно (все в норме [math]) в [math], достаточно взять частичные суммы ряда Фурье.
2.Множество [math] непр. функций, обращающихся в 0 в нуле, плотно во множестве непрерывных функций, достаточно исправить график каждой на малом отрезке [math] .
3.Множество многочленов плотно в указанном множестве [math] непрерывных функций в равномерной норме, по Теореме Вейерштрасса. Тогда если [math] и [math] то [math] и [math], значит, нашелся и приближающий многочлен со значением 0 в нуле [math] Раз он приближает в равномерной норме, то и в норме [math]
Отсюда, многочлены с нулевым свободным членом плотны в [math] , только нулевая f может быть
Простые с виду вопросы про L2(0,1)
Ian писал(а):Source of the post Тут я подобрал функцию, но доказать, что максимум отношения норм на ней. не могу
Найдем собственные значения и вектора
Тогда
и
Отсюда
Остается провести оптимизацию по
Замечание: Тут небольшая путаница. Под "sign" я имел ввиду функцию Хевисайда (0 для отрицательных, 1 для положительных).
Последний раз редактировалось zykov 24 июн 2018, 13:35, всего редактировалось 1 раз.
Простые с виду вопросы про L2(0,1)
Кроме косинуса ещё можно экспоненты попробовать (линейную комбинацию "плюс" и "минус" экспонент), но они меньше дают.
Простые с виду вопросы про L2(0,1)
Из  получаем
получаем  . Остаются только тригонометрический и гиперболический косинусы.
. Остаются только тригонометрический и гиперболический косинусы.
Из получаем
получаем 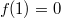 . Отсюда остается только тригонометрический косинус и
. Отсюда остается только тригонометрический косинус и  . Наибольшую
. Наибольшую  даёт
даёт 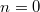 .
.
Из
Простые с виду вопросы про L2(0,1)
Я тоже получил это вчера короче, вариационным исчислением (не факт, что студенты, которым это задали, его уже проходили). Обозначим [math], тогда имеем задачу на условный экстремумzykov писал(а):и.
[math]
[math]
[math]
Из уравнения Эйлера-Лагранжа сразу тогда
[math], среди экспонент [math] решение [math]
, среди тригонометрических [math] решение [math]
Дальше тупо подстановкой в отношение интегралов оптимизация по [math], которая у меня не получилась почему-то.
Простые с виду вопросы про L2(0,1)
Все-таки в задаче 1 и Вы пользовались тем, что изучается позднее в курсе ФА (что норма симметричного интегрального оператора равна максимуму из собственных чисел). И наверное никогда не узнаем, какое решение имелось в виду.
И почему все-таки не проходит тупая оптимизация в лоб, трансцендентные функции получаются? Ответ [math] оптимальный, маткад это подтверждает
И почему все-таки не проходит тупая оптимизация в лоб, трансцендентные функции получаются? Ответ [math] оптимальный, маткад это подтверждает
Простые с виду вопросы про L2(0,1)
Ian писал(а):Source of the post И почему все-таки не проходит тупая оптимизация в лоб,
А как её сделать? Там же не значение нужно найти, и не вектор, а функцию. Это задача для вариационного исчисления.
Можно конечно прооптимизировать вектор для конечной сетки (100 или 1000 точек, вместо интеграла будет сумма). Что я и сделал на компьютере. Получил что-то очень близкое к косинусу. Это конечно намёк на решение, но не оно само.
Простые с виду вопросы про L2(0,1)
Ian писал(а):Source of the post Я тоже получил это вчера короче, вариационным исчислением (не факт, что студенты, которым это задали, его уже проходили). Обозначим, тогда имеем задачу на условный экстремум
Да кстати. Через вариационное проще. Я тоже сначала через него начал, но запутался (делал для
Отсюда
И получаем
Простые с виду вопросы про L2(0,1)
Это очень удачно вышло, что из граничного условия на одном конце вывелось граничное на другом. Тогда конечно оптимальная [math] очевидна.Спасибо!zykov писал(а):Отсюда
Простые с виду вопросы про L2(0,1)
Продолжение сериала, оттуда же
3.Найти норму оператора в [math]
[math]
Даже вар. исчисление не сработало, и ответа не знаю
3.Найти норму оператора в [math]
[math]
Даже вар. исчисление не сработало, и ответа не знаю
Простые с виду вопросы про L2(0,1)
Вольфрам выдал здесь вместо косинуса что-то вроде
 , где
, где 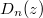 - параболическая цилиндрическая функция.
- параболическая цилиндрическая функция.
Простые с виду вопросы про L2(0,1)
wolframalpha ? посмотреть бы как ставилась задача
Простые с виду вопросы про L2(0,1)
Так же, как и раньше.

[math]
[math]
Тогда . Вольфрам решает этот диф.ур и выражает через функции Бесселя и Гамма.
. Вольфрам решает этот диф.ур и выражает через функции Бесселя и Гамма.
Я обозначил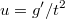 , тогда
, тогда  и
и  . Отсюда
. Отсюда 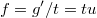 и
и  .
.
Из второго вольфрам выражает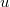 через цилиндрические параболические функции (https://www.wolframalpha.com/input/?i=u ... +t%5E2%3D0). Чтобы получить
через цилиндрические параболические функции (https://www.wolframalpha.com/input/?i=u ... +t%5E2%3D0). Чтобы получить 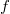 , умножаем
, умножаем 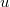 на
на 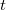 .
.
[math]
[math]
Тогда
Я обозначил
Из второго вольфрам выражает
Простые с виду вопросы про L2(0,1)
Да, ответ неэлементарный, но какая же точно норма?. Я когда увидел эту задачу-только оценил
По неравенству Коши-Буняковского
[math]
[math]
Поэтому
[math]
По неравенству Коши-Буняковского
[math]
[math]
Поэтому
[math]
Простые с виду вопросы про L2(0,1)
Для старой задачи ответ был  . Численный анализ по 1000 точек (собственные значения дискретной матрицы) выдавал
. Численный анализ по 1000 точек (собственные значения дискретной матрицы) выдавал 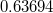 , т.е. точность 3 знака.
, т.е. точность 3 знака.
Для новой задачи по 1000 точек выдаёт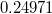 . (Для сравнения
. (Для сравнения  .)
.)
Для новой задачи по 1000 точек выдаёт
Простые с виду вопросы про L2(0,1)
Собственный вектор для 1000 точек выглядит примерно так:
Простые с виду вопросы про L2(0,1)
Красиво. Сразу ассоциируется с Бесселем. На этом пути можно и точное значение нормы поискать.
1. Задаем большое N.
2.Берем нижнетреугольную матрицу [math]
, соответствует преобразованию
[math] численного интегрирования [math], с точностью до множителя [math]
3.Составляем [math] и находим у нее наибольшее собственное число [math]
Может аналитически выражаться, очень простая матрица.
4. Тогда
[math]
1. Задаем большое N.
2.Берем нижнетреугольную матрицу [math]
Код: Выбрать все
1
1 2
1 2 3
......
1 2 3 ... N[math] численного интегрирования [math], с точностью до множителя [math]
3.Составляем [math] и находим у нее наибольшее собственное число [math]
Может аналитически выражаться, очень простая матрица.
4. Тогда
[math]
-
peregoudov
- Сообщений: 620
- Зарегистрирован: 29 дек 2015, 13:17
Простые с виду вопросы про L2(0,1)
А почему нельзя использовать тот же подход, что в предыдущем случае, просто с заменой  ? Или даже без замены, но тогда получается уравнение третьего порядка для
? Или даже без замены, но тогда получается уравнение третьего порядка для 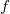 .
.
Вообще численное значение весьма смахивает на 1/4...
Вообще численное значение весьма смахивает на 1/4...
Кто сейчас на форуме
Количество пользователей, которые сейчас просматривают этот форум: нет зарегистрированных пользователей и 2 гостей