[math]
При [math] : по формуле дополнения для гамма-функции
[math] и может возьмется.
Но в задачнике, не знаю каком, утверждается, что он выражается компактно при любом [math], не обязательно целом
Интеграл
Интеграл
Возможно получится, если использовать определение по Вейерштрассу: [math].
Логарифм превращает произведение в сумму. А интегралы от отдельных слагаемых берутся.
Результат будет в виде бесконечной суммы, что уже "компактно".
Возможно и саму сумму можно посчитать и выразить конечной формулой.
Логарифм превращает произведение в сумму. А интегралы от отдельных слагаемых берутся.
Результат будет в виде бесконечной суммы, что уже "компактно".
Возможно и саму сумму можно посчитать и выразить конечной формулой.
Интеграл
Вольфрам на вебе осилил частную сумму
https://www.wolframalpha.com/input/?i=sum(((2*n%5E2%2B(2*a%2B2)*n)*log((n%2Ba%2B1)%2Fn)%2B(-2*n%5E2-2*a*n)*log((n%2Ba)%2Fn)-2*n-2*a-1)%2Fn,n,1,inf)
Значит и предел должен найтись.
https://www.wolframalpha.com/input/?i=sum(((2*n%5E2%2B(2*a%2B2)*n)*log((n%2Ba%2B1)%2Fn)%2B(-2*n%5E2-2*a*n)*log((n%2Ba)%2Fn)-2*n-2*a-1)%2Fn,n,1,inf)
Значит и предел должен найтись.
-
peregoudov
- Сообщений: 620
- Зарегистрирован: 29 дек 2015, 13:17
Интеграл
Обозначим
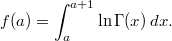
Тогда ,
,  .
.
Тогда
Интеграл
Да.
Совсем просто!
Совсем просто!
Интеграл
Несколько посложнее:  - целое между
- целое между  и
и  , тогда
, тогда 


...
 .
.
...
Интеграл
Ну мастера, что тут еще сказать...Всем спасибо!
-
peregoudov
- Сообщений: 620
- Зарегистрирован: 29 дек 2015, 13:17
Интеграл
Мне  какую-то функцию Грина напоминает, никак не могу вспомнить... Это я к вопросу об интеграле при a=0.
какую-то функцию Грина напоминает, никак не могу вспомнить... Это я к вопросу об интеграле при a=0.
Интеграл
zykov писал(а):Source of the post Вольфрам выдал.
Попробовал в Maxima (поставил себе на компьютер, а то вольфрам на вебе постоянно отказывается считать).
Прямо интеграл от гамма-функции не считает, но от синуса посчитал и выдал такой же.
Интеграл
peregoudov писал(а):Source of the post Мнекакую-то функцию Грина напоминает, никак не могу вспомнить.
Собственно Вольфрам тут то же выдал:
Здесь
Интеграл
Неужели нельзя исхитриться посчитать без спецфункций, даже при том, что первообразная неэлементарна. В задачнике же задано, значит надеются на точный ответ.Свелось к такому:
[math]
https://www.wolframalpha.com/input/?i=%5Cint_0%5E(pi%2F2)(t*ctg(t)*dt)
[math]
https://www.wolframalpha.com/input/?i=%5Cint_0%5E(pi%2F2)(t*ctg(t)*dt)
Интеграл
Если брать неопределенный интеграл, то без полилогарифма не обойтись.

Возможно определенный интеграл и можно как-то посчитать без неё (в формуле неопределнного эти
и можно как-то посчитать без неё (в формуле неопределнного эти 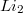 взаимно уничтожаются в
взаимно уничтожаются в 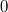 , и в
, и в 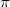 ).
).
Когда давно был студентом, мы на ТФКП брали разные определенные интегралы заменой контура на комплексной плоскости и получалось взять сложные интегралы. Может и здесь такой трюк сработает.
Возможно определенный интеграл
Когда давно был студентом, мы на ТФКП брали разные определенные интегралы заменой контура на комплексной плоскости и получалось взять сложные интегралы. Может и здесь такой трюк сработает.
Интеграл
Ian писал(а):Source of the post Неужели нельзя исхитриться посчитать без спецфункций
Ха, гугл знает всё! Даже это.
По запросу "integrate log sin x" первая ссылка "Integrate log(sinx) from 0 to pi /2?".
Интеграл
Действительно простой прием. Только объяснение там сумбурное.[math]
[math]
[math]
Окончательно [math]
[math]
[math]
Окончательно [math]
Кто сейчас на форуме
Количество пользователей, которые сейчас просматривают этот форум: нет зарегистрированных пользователей и 1 гость