Бред про регрессии
Бред про регрессии
По выборке трехмерной случайной величины [math] получено уравнение регрессии [math] с [math] и уравнение регрессии [math] с [math]. Каково уравнение регрессии [math] и с каким коэффициентом детерминации [math]?
-
peregoudov
- Сообщений: 620
- Зарегистрирован: 29 дек 2015, 13:17
Бред про регрессии
Пусть  и пусть уравнения регрессии записаны в виде
и пусть уравнения регрессии записаны в виде  ,
, 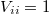 . Пусть ковариационная матрица
. Пусть ковариационная матрица
равна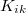 , через
, через  обозначим ее
обозначим ее 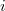 -й столбец. По видимому, речь идет о регрессиях с максимальным коэффициентом детерминации. Тогда введенные величины удовлетворяют уравнениям
-й столбец. По видимому, речь идет о регрессиях с максимальным коэффициентом детерминации. Тогда введенные величины удовлетворяют уравнениям


В принципе, имеем 9 уравнений для 9 неизвестных: 6 компонент ковариационной матрицы, два коэффициента регресии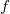 и
и 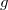 и коэффициент детерминации
и коэффициент детерминации 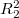 . Однако ковариационная матрица входит в уравнения линейно, поэтому определена с точностью до множителя. Шесть уравнений (четыре из первого множества при
. Однако ковариационная матрица входит в уравнения линейно, поэтому определена с точностью до множителя. Шесть уравнений (четыре из первого множества при 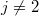 и два из второго при
и два из второго при 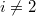 ) образуют однородную линейную систему для
) образуют однородную линейную систему для 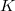 . Вот ее определитель (он выражается через
. Вот ее определитель (он выражается через  ,
,  ,
,  ,
, 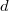 ,
, 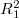 .
. 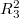 ), вообще говоря, отличен от нуля. Так что нужно накладывать на исходные данные какое-то дополнительное условие... Плюс еще положительную определенность
), вообще говоря, отличен от нуля. Так что нужно накладывать на исходные данные какое-то дополнительное условие... Плюс еще положительную определенность 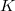 нужно как-то обеспечить...
нужно как-то обеспечить...
P. S. Ну вот, как вариант: можно все выразить через ковариационную матрицу

равна
В принципе, имеем 9 уравнений для 9 неизвестных: 6 компонент ковариационной матрицы, два коэффициента регресии
P. S. Ну вот, как вариант: можно все выразить через ковариационную матрицу
Бред про регрессии
Да, естественно коэффициенты линейной регрессии искались, и надо найти, по МНК, что равносильно искать максимум коэффициента детерминации. Но тут нельзя бездумно все формулы которые есть в теории, применять, они выведены для регрессий со свободными членами а мы полагаем, что они нули (это так на всякий случай)
Выборки x,y,z можно интерпретировать как вектора n-мерного евклидова пространства. Но так как в нем на любые три вектора можно натянуть трехмерное пространство, смотрим в нем. Первая регрессия -это разложение проекции x на плоскость Oyz по векторам y и z, а ее коэффициент детерминации это [math] угла между х и плоскостью Oyz. Вторая регрессия дает еще пару аналогичных данных. Задача свелась к стереометрической, хотя некоторые данные и буквы
Выборки x,y,z можно интерпретировать как вектора n-мерного евклидова пространства. Но так как в нем на любые три вектора можно натянуть трехмерное пространство, смотрим в нем. Первая регрессия -это разложение проекции x на плоскость Oyz по векторам y и z, а ее коэффициент детерминации это [math] угла между х и плоскостью Oyz. Вторая регрессия дает еще пару аналогичных данных. Задача свелась к стереометрической, хотя некоторые данные и буквы
-
peregoudov
- Сообщений: 620
- Зарегистрирован: 29 дек 2015, 13:17
Бред про регрессии
О свободных членах я действительно не думал, но ничего нового и тем более хорошего они не несут.
Ок, давайте начнем сначала. Я пользуюсь определением из Википедии. Пусть уравнения регрессии записываются в виде ,
, 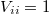 , а среднее значение вектора пусть равно
, а среднее значение вектора пусть равно  . Ковариационную матрицу по-прежнему обозначаем через
. Ковариационную матрицу по-прежнему обозначаем через 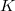 . Тогда полная дисперсия
. Тогда полная дисперсия 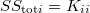 , а остаточная
, а остаточная

Минимум остаточной дисперсии (а значит максимум коэффициента детерминации) достигается при

При этом для самого коэффициента детерминации получаем соотношение

Ну, то есть, если вы хотите сказать, что уравнения регрессии получились однородными, а не выбирались таковыми изначально, то ничего, собственно, не меняется, просто из условий можно сделать вывод, что (он перпендикулярен трем линейно независимым векторам
(он перпендикулярен трем линейно независимым векторам  ).
).
Вторая возможность состоит в том, чтобы сразу искать однородное уравнение регрессии . Тогда, вводя матрицу простых средних
. Тогда, вводя матрицу простых средних 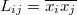 , получаем
, получаем 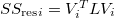 , так что все уравнения остаются справедливы с заменой
, так что все уравнения остаются справедливы с заменой 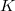 на
на
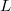 , кроме как в полной дисперсии
, кроме как в полной дисперсии

Ну вот, у нас просто появились три новые неизвестные и никаких дополнительных уравнений. Опять-таки, полагая , возвращаемся к исходным уравнениям.
, возвращаемся к исходным уравнениям.
Но это все лирика. Вы утверждаете, что у вас, якобы, есть какое-то "стереометрическое решение". Ну и чему у вас равна ковариационная матрица в случае a=1, b=1, c=1, d=1?
Ок, давайте начнем сначала. Я пользуюсь определением из Википедии. Пусть уравнения регрессии записываются в виде
Минимум остаточной дисперсии (а значит максимум коэффициента детерминации) достигается при
При этом для самого коэффициента детерминации получаем соотношение
Ну, то есть, если вы хотите сказать, что уравнения регрессии получились однородными, а не выбирались таковыми изначально, то ничего, собственно, не меняется, просто из условий можно сделать вывод, что
Вторая возможность состоит в том, чтобы сразу искать однородное уравнение регрессии
Ну вот, у нас просто появились три новые неизвестные и никаких дополнительных уравнений. Опять-таки, полагая
Но это все лирика. Вы утверждаете, что у вас, якобы, есть какое-то "стереометрическое решение". Ну и чему у вас равна ковариационная матрица в случае a=1, b=1, c=1, d=1?
Бред про регрессии
Не утверждаю. В стадии поиска самого удобного представления данных задачи, при том что разрешимость и корректность задачи неизвестна. Вот так делаю, тоже понятно через ковар. матрицуperegoudov писал(а):Но это все лирика. Вы утверждаете, что у вас, якобы, есть какое-то "стереометрическое решение". Ну и чему у вас равна ковариационная матрица в случае a=1, b=1, c=1, d=1?
Система нормальных уравнений для 1-й регрессии
[math]
Чтобы превратить это в матричное уравнение, добавим равенство, служащее определением коэффициента детерминации[math]
Получили типа ковариационной матрицы, умноженной на известный столбец. Аналогично поступим со второй известной регрессией и с неизвестной. Получаем уравнение в матрицах
[math]
Отсюда не следует, что матрица с неизвестными f,g- симметрична, хотя остальные две и симметричны. Но хотя бы собрали в одно уравнение, полностью содержащее все данные , искомые и связи между ними.
-
peregoudov
- Сообщений: 620
- Зарегистрирован: 29 дек 2015, 13:17
Бред про регрессии
А, ну то есть пришли к тому же, что написано в моем первом сообщении.
Бред про регрессии
peregoudov писал(а):А, ну то есть пришли к тому же, что написано в моем первом сообщении.
Конечно! А я и не сомневался. Но я хотя бы сохраняю единство обозначений а без этого не пойму что пишут.Хорошую формулу не плохо и два раза повторить)
-
peregoudov
- Сообщений: 620
- Зарегистрирован: 29 дек 2015, 13:17
Бред про регрессии
Я тоже много времени потратил на то, чтобы в приличном виде описать ограничения на исходные данные. Ничего не выходит. Поэтому думаю, тут только конкретные числа в качестве a, b, c, d можно задать, так, чтобы задача решалась. Но красоты никакой... Еще не вполне исследовал случай равных коэффициентов детерминации --- там формулы упрощаются, может, можно что-то нарыть...
Мне бы ваши проблемы.Ian писал(а):Source of the post Но я хотя бы сохраняю единство обозначений а без этого не пойму что пишут.
Бред про регрессии
У Вас прозвучало, что задача скорей всего не имеет красивого ответа. Я думаю, что даже доказательство того, что задача имеет хотя бы один ответ (не приводя его), это уже актуально, может быть - ново, и тогда по определению красиво. В эконометрике (которая макро-, ну там ВВП, нац.доход, инвестиции/потребление) недостатка в статистике нет, и принято считать что что угодно может оказаться как зависимым фактором, так и независимым.Пишутся всевозможные системы эконометрических уравнений, та система 2 ур. с 3 неизв., которая у нас, считается переопределенной (противоречивой). С другой стороны, раз уж у двух уравнений указаны меры их достоверности, то не обязательно противоречие, такое случиться могло при некоторых [math] . Более того, такие высокие коэффициенты детерминации это редкость для отрасли, такие уравнения игнорировать не хочется. Вот и появился такой допвопрос студенту-заочнику на троечку, а знает ли преподаватель-экономист корректный математический ответ на свой вопрос, теперь не узнаем. Если тройки [math] и [math] "сильно непропорциональны" друг другу, то скорей всего, противоречие уже в условии, таких больших [math] получиться одновременно не могло. Так определить хотя бы границы множества возможных [math].
Бред про регрессии
Обозначим углы между векторами [math],тогда удается исключить [math] вообще
[math]
Более того, и коэффициенты детерминации все выражаются через [math]
Для выражения [math] рассмотрим вектора [math], пусть вектор [math] ортогонален как [math], так и [math], то есть H- проекция OX на плоскость YOZ. Введем [math]-проекцию X на OY
[math] (Заменяем косинус двугранного угла [math] по первой теореме косинусов https://ru.wikipedia.org/wiki/Трёхгранный_угол ) [math] M ввел для краткости
[math]
[math]
Более того, и коэффициенты детерминации все выражаются через [math]
Для выражения [math] рассмотрим вектора [math], пусть вектор [math] ортогонален как [math], так и [math], то есть H- проекция OX на плоскость YOZ. Введем [math]-проекцию X на OY
[math] (Заменяем косинус двугранного угла [math] по первой теореме косинусов https://ru.wikipedia.org/wiki/Трёхгранный_угол ) [math] M ввел для краткости
[math]
-
peregoudov
- Сообщений: 620
- Зарегистрирован: 29 дек 2015, 13:17
Бред про регрессии
Ну, во-первых, у вас просто арифметические ошибки. Если разделить строки на 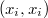 никаких косинусов, конечно, не выйдет, потому что косинус --- это не
никаких косинусов, конечно, не выйдет, потому что косинус --- это не 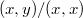 , а
, а 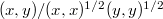 . Но получить вожделенные косинусы можно, только придется умножить матрицу коэффициентов уравнений регрессии на
. Но получить вожделенные косинусы можно, только придется умножить матрицу коэффициентов уравнений регрессии на 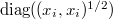 слева и
слева и 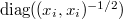 справа. Непонятно, правда, зачем...
справа. Непонятно, правда, зачем...
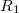 и
и 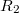 . Но это не все, конечно, потому что в результате решения должна еще получиться положительно определенная матрица.
. Но это не все, конечно, потому что в результате решения должна еще получиться положительно определенная матрица.
Так вроде написал уже: просто для разрешимости системы шести однородных уравнений для ковариационной матрицы должно выполняться одно условие (равенство нулю определителя), включающее a, b, c, d,Ian писал(а):Source of the post Так определить хотя бы границы множества возможных (a,b,c,d).
-
peregoudov
- Сообщений: 620
- Зарегистрирован: 29 дек 2015, 13:17
Бред про регрессии
В общем, самое простое, что получилось: использовать соотношения
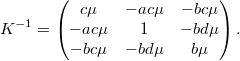
Здесь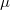 --- параметр,
--- параметр, 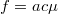 ,
, 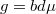 , а коэффициенты детерминации выражаются формулами
, а коэффициенты детерминации выражаются формулами
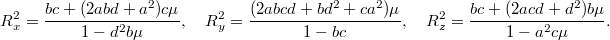
И есть требование положительной определенности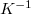

Отсюда следуют такие ограничения:

Отмечу, что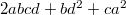 является положительно определенной квадратичной формой переменных
является положительно определенной квадратичной формой переменных 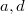 при
при 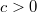 и отрицательно определенной при
и отрицательно определенной при 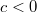 . Соответственно, в первом случае
. Соответственно, в первом случае
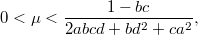
а во втором
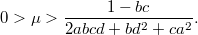
Собственно, все. При выполнении указанных неравенств на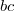 и
и 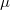 ковариационная матрица существует и положительно определена. Отмечу еще, что
ковариационная матрица существует и положительно определена. Отмечу еще, что 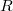 являются возрастающими функциями
являются возрастающими функциями  . Формулу для
. Формулу для 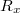 можно еще записать так
можно еще записать так
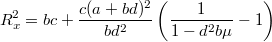
(аналогично для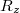 с заменой
с заменой  ,
,  ). При
). При 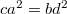 имеем
имеем 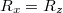 независимо от
независимо от 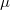 , в противном случае
, в противном случае  независимо от
независимо от 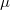 (за исключением концов допустимого интервала).
(за исключением концов допустимого интервала).
P. S. Ну, вот так как-то выглядит зависимость коэффициентов детерминации от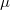 . Сосчитано для a=-0.1, b=0.8, c=0.5, d=0.3.
. Сосчитано для a=-0.1, b=0.8, c=0.5, d=0.3.
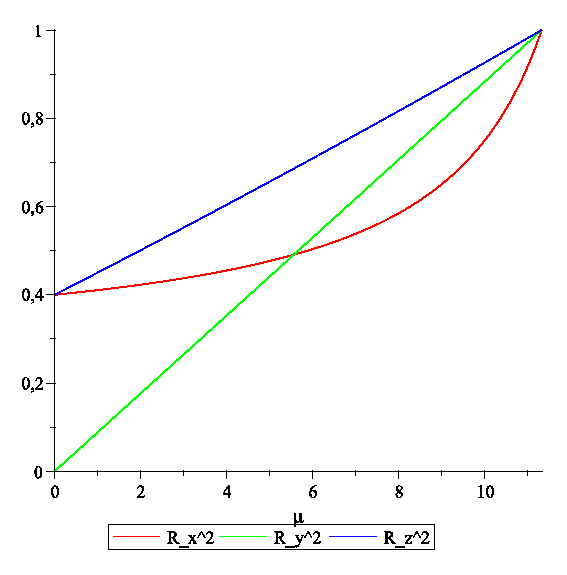
и параметризовать обратную ковариационную матрицу
Здесь
И есть требование положительной определенности
Отсюда следуют такие ограничения:
Отмечу, что
а во втором
Собственно, все. При выполнении указанных неравенств на
(аналогично для
P. S. Ну, вот так как-то выглядит зависимость коэффициентов детерминации от

Бред про регрессии
Ну я подытожу от себя. Название темы удачное, в том смысле что я писал в ней бред, а Вы выкладывали нормальный контент. Который, однако, мной не понят и я не могу ответить по существу. Но если принять, что мы тут пишем для потомков, то это не должно Вас сильно волновать, тема не хуже других здесь открытых, ни по актуальности, ни по количеству труденостей. уже преодоленных участниками. Спасибо за ответы!
Кто сейчас на форуме
Количество пользователей, которые сейчас просматривают этот форум: нет зарегистрированных пользователей и 1 гость