Надо доказать что группы [math]-группа перестановок трех элементов, и группа [math]-группа матриц 2х2 с элементами -двоичными числами, имеющих определитель 1, -изоморфны
В каждой группе 6 элементов, из них два порядка 3(в S3 это циклы) и три порядка 2 (в S3 это транспозиции). Ввиду таких маленьких групп изоморфизм я построил, просто сопоставив таблицы умножения (таблицы Кэли).Для S3 она кстати графически изображена в вики https://ru.wikipedia.org/wiki/Симметрическая_группа Но традиционный способ доказательства изоморфизма -придумать этим группам одинаковые представления. Ума не приложу какие тут могут быть. И надеюсь на Peregoudov, постоянно ими пользуется, видимо книгу прочитал которой у меня нет)
Изоморфизм группы S3
-
peregoudov
- Сообщений: 620
- Зарегистрирован: 29 дек 2015, 13:17
Изоморфизм группы S3
Эээ... Насколько я понимаю, изоморфизм как раз определяется как отображение групп, сохраняющее таблицу умножения. Поэтому построение такого отображения --- самый прямой способ доказательства и есть.
А про "одинаковые представления"... даже не знаю. Любая группа имеет тривиальное представление --- единичное. Отсюда ведь не следует, что все группы изоморфны... Поэтому тут речь должна, видимо, не об одном наугад взятом представлении идти, а о полном наборе неприводимых представлений или о каком-то вполне определенном (присоединенном?). Честно скажу, не знаю теорем о восстановлении группы по представлениям. Кажется, по присоединенному можно восстановить, потому что это, считай, просто по-другому записанная таблица умножения группы.
И есть еще одна проблема: не понял я, что такое
 Двоичные числа --- это 0 и 1? Из таких, действительно, можно построить 6 матриц с ненулевым определителем. А арифметика у них по модулю 2? Тогда, похоже, действительно группа получается. И вы, наверное, хотите описать действие этой группы на некие объекты как перестановки? Думаю, надо взять какие-то матрицы 2х2 с ограничением, так, чтобы независимых элементов было 3. В общем, догадки мои прокомментируйте, тогда буду думать дальше.
Двоичные числа --- это 0 и 1? Из таких, действительно, можно построить 6 матриц с ненулевым определителем. А арифметика у них по модулю 2? Тогда, похоже, действительно группа получается. И вы, наверное, хотите описать действие этой группы на некие объекты как перестановки? Думаю, надо взять какие-то матрицы 2х2 с ограничением, так, чтобы независимых элементов было 3. В общем, догадки мои прокомментируйте, тогда буду думать дальше.
А про "одинаковые представления"... даже не знаю. Любая группа имеет тривиальное представление --- единичное. Отсюда ведь не следует, что все группы изоморфны... Поэтому тут речь должна, видимо, не об одном наугад взятом представлении идти, а о полном наборе неприводимых представлений или о каком-то вполне определенном (присоединенном?). Честно скажу, не знаю теорем о восстановлении группы по представлениям. Кажется, по присоединенному можно восстановить, потому что это, считай, просто по-другому записанная таблица умножения группы.
И есть еще одна проблема: не понял я, что такое
Изоморфизм группы S3
Да, двоичные числа это 0 и 1 так что 1=1=0, применяется как при перемножении матриц, так и при вычислении определителя. Матрицы
01
11
и
11
10 - те две матрицы из 6, которые в кубе равны единичной и значит при изоморфизме должны получаться из циклов. Еще три матрицы -из транспозиций, а единичная, понятно, из тождественной перестановки.
Да, хотелось бы понять почему группа матриц то же самое, что группа перестановок трех элементов.
Еще один путь -факторизовать по группе порядка 3 и получить фактор-группу порядка 2, доказать два изоморфизма. Но единственная подгруппа - нормальный делитель это группа четных перестановок (единичная и два цикла), но надо же и доказать, что и группа трех матриц, единичная и две указанных выше -это нормальный делитель (а то нельзя факторизовать), а это так же трудоемко, как упорядочение таблиц умножения.А после этого из изоморфизма подгрупп порядка 3 и изоморфизма факторгрупп порядка 2 сразу следует изоморфизм и самих групп.
01
11
и
11
10 - те две матрицы из 6, которые в кубе равны единичной и значит при изоморфизме должны получаться из циклов. Еще три матрицы -из транспозиций, а единичная, понятно, из тождественной перестановки.
Да, хотелось бы понять почему группа матриц то же самое, что группа перестановок трех элементов.
Еще один путь -факторизовать по группе порядка 3 и получить фактор-группу порядка 2, доказать два изоморфизма. Но единственная подгруппа - нормальный делитель это группа четных перестановок (единичная и два цикла), но надо же и доказать, что и группа трех матриц, единичная и две указанных выше -это нормальный делитель (а то нельзя факторизовать), а это так же трудоемко, как упорядочение таблиц умножения.А после этого из изоморфизма подгрупп порядка 3 и изоморфизма факторгрупп порядка 2 сразу следует изоморфизм и самих групп.
-
peregoudov
- Сообщений: 620
- Зарегистрирован: 29 дек 2015, 13:17
Изоморфизм группы S3
А, не, все очень просто! Рассмотрим векторы (1,0), (0,1) и (1,1) из тех же "двоичных чисел". Тогда матрицы группы действуют на них, как перестановки, например
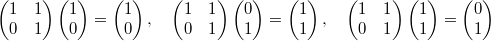
--- перестановка второго и третьего векторов.
--- перестановка второго и третьего векторов.
Изоморфизм группы S3
Спасибо за главную идею!Тогда уж рассмотрим матрицу 2х3 из этих векторов , расположенных по столбцам, и как умножение слева на матрицу из группы переставляет столбцы этой матрицы. Главное что в нулевой столбец ни один столбец ни одна матрица не переводитperegoudov писал(а):А, не, все очень просто! Рассмотрим векторы (1,0), (0,1) и (1,1) из тех же "двоичных чисел". Тогда матрицы группы действуют на них, как перестановки, например
--- перестановка второго и третьего векторов.
Кто сейчас на форуме
Количество пользователей, которые сейчас просматривают этот форум: нет зарегистрированных пользователей и 1 гость