В плоском случае, ответ, как известно,
Среднее по сферическому треугольнику
-
peregoudov
- Сообщений: 620
- Зарегистрирован: 29 дек 2015, 13:17
Среднее по сферическому треугольнику
Сферический треугольник задан своими вершинами  ,
,  ,
,  (
(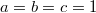 ). Найти среднее значение вектора
). Найти среднее значение вектора 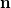 (
(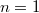 ) по этому треугольнику.
) по этому треугольнику.
В плоском случае, ответ, как известно, .
.
В плоском случае, ответ, как известно,
Среднее по сферическому треугольнику
Ну среднее векторов уже не будет на сфере, оно будут внутри шара.
Кроме того 3 вершини зададут не 1, а 2 комплементарных треугольника. Так например, если все три лежат в одной плоскости с центром шара, то они разабъют сферу на две полусферы. Средние по полусферам не будут зависить от конкретных значений векторов.
Вообще мне кажется, тут нет простого решения. Нужно "в лоб" интегрировать и получится что-то страшное.
Кроме того 3 вершини зададут не 1, а 2 комплементарных треугольника. Так например, если все три лежат в одной плоскости с центром шара, то они разабъют сферу на две полусферы. Средние по полусферам не будут зависить от конкретных значений векторов.
Вообще мне кажется, тут нет простого решения. Нужно "в лоб" интегрировать и получится что-то страшное.
Среднее по сферическому треугольнику
Рассмотрим вырождающийся треугольник c [math], все таки на почти такие треугольники можно разбить любой. Обозначим [math] расстояние по дуге от конца вектора a до точки х в нем, тогда ширина треугольника в точке х порядка [math], площадь треугольника порядка [math]
Проведем комплексную плоскость с действительной осью вдоль a через ось треугольника, тогда положение вектора среднего в этой плоскости находится как [math] легко берется, в частности, при [math] получается точка [math]
Проведем комплексную плоскость с действительной осью вдоль a через ось треугольника, тогда положение вектора среднего в этой плоскости находится как [math] легко берется, в частности, при [math] получается точка [math]
-
peregoudov
- Сообщений: 620
- Зарегистрирован: 29 дек 2015, 13:17
Среднее по сферическому треугольнику
Ответ должен быть простым и симметричным по перестановке a, b, c, и хотелось бы при интегрировании эту симметрию явно сохранить. В общем, из соображений симметрии ответ есть линейная комбинация  ,
,  ,
,  с коэффициентами, зависящими от
с коэффициентами, зависящими от  ,
,  ,
,  . Там на самом деле всего одна функция трех переменных, к тому же симметричная по паре аргументов. Или --- тут есть интересная связь с другой обсуждавшейся задачей --- две функции, построенные по диаграммам Юнга "3 в ряд" и "буквой г".
. Там на самом деле всего одна функция трех переменных, к тому же симметричная по паре аргументов. Или --- тут есть интересная связь с другой обсуждавшейся задачей --- две функции, построенные по диаграммам Юнга "3 в ряд" и "буквой г".
Вот самое простое, что у меня получилось для прямого интегрирования. Пусть (без ограничения общности) все векторы ,
,  ,
,  направлены в верхнюю полусферу. Спроецируем иx и вектор
направлены в верхнюю полусферу. Спроецируем иx и вектор 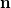 на горизонтальную плоскость, касающуюся сферы в верхней точке, то есть введем векторы
на горизонтальную плоскость, касающуюся сферы в верхней точке, то есть введем векторы  ,
, 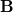 ,
,  ,
,  , концы которых лежат в указанной плоскости и
, концы которых лежат в указанной плоскости и  , ... Нетрудно сосчитать, что
, ... Нетрудно сосчитать, что 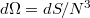 . Раскладывая вектор
. Раскладывая вектор  на единичный вертикальный вектор
на единичный вертикальный вектор  и горизонтальный вектор
и горизонтальный вектор  , можно записать
, можно записать

И задача сводится к среднему по плоскому треугольнику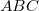 , только не просто для вектора.
, только не просто для вектора.
Вот самое простое, что у меня получилось для прямого интегрирования. Пусть (без ограничения общности) все векторы
И задача сводится к среднему по плоскому треугольнику
Кто сейчас на форуме
Количество пользователей, которые сейчас просматривают этот форум: нет зарегистрированных пользователей и 2 гостей