Улучшить точность при двукратном измерении

peregoudov · Сообщение **peregoudov** » 15 мар 2017, 11:16

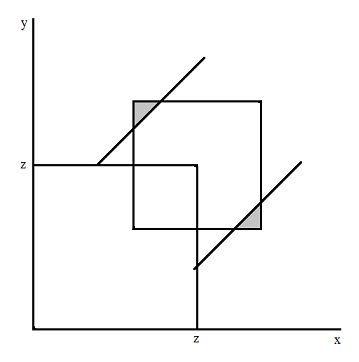
Не дают мне покоя мои "нефтяники". Теперь требуют, чтобы я развил идею, которая, на первый (да и на второй) взгляд, выглядит абсолютно бредовой.

Двумя приборами измеряется некоторая величина. Как водится, предполагается, что результаты измерений есть независимые случайные величины, распределенные по нормальному закону около истинного значения с некоторой дисперсией, определяемой точностью прибора. Для простоты предполагается, что точности приборов одинаковы. Итак, на входе мы имеет три числа: результаты измерений $x$

,

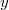
и дисперсию $\sigma$ .

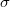
Обычный способ обработки измерений состоит в вычислении среднего $(x+y)/2$

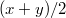
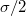
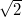
--- именно оно принимается за оценку измеренного значения. Элементарно показывается, что это случайная величина, которая распределена вокруг истинного значения по нормальному же закону, но уже с дисперсией $\sigma/2$ , то есть точность определения величины увеличивается в $\sqrt2$ раз.

Так вот, безумная идея состоит в том, что точность можно улучшить гораздо сильнее (заявляются значения в 5 раз :shock:

) --- за счет отбрасывания "неподходящих" измерений. Утверждается, что есть программа, которая принимает указанные выше три значения, и, пошуршав мозгами, выдает некоторую оценку измеряемой величины и флажок, является ли введенный набор значений "подходящим". Утверждается, что тестирование этой программы на искусственно сгенерированных случайных числах (результатах "измерений"), при условии, что усреднение ведется только по "подходящим" измерениям, показывает, что дисперсия выдаваемой оценки уменьшается в 4-25 раз по сравнению с дисперсией одного прибора, то есть уменьшается существенно сильнее, чем при вычислении простого среднего из двух измерений. Бредовость идеи косвенно подтверждается тем обстоятельством, что "подходящими" измерениями часто оказываются такие, когда $x$

и

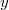
лежат по одну сторону от истинного значения, а выдаваемая программой оценка лежит вне интервала $(x,y)$

.

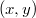
В связи с этим напрашивается следующая постановка задачи. Пусть $x$

и

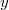
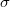
--- две независимые случайные величины, распределенные по нормальному закону с одинаковой дисперсией $\sigma$ вокруг некоторого истинного значения $z$

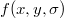
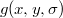
. Пусть $f(x,y,\sigma)$ --- некоторая оценка истинного значения, а $g(x,y,\sigma)$ --- некоторый критерий отбора. Вопрос: как наилучшим образом выбрать $f$

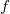
и

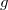
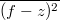
, чтобы "дисперсия по критерию" $\overline{(f-z)^2}$ была минимальной независимо от $z$

? Усреднение производится по мере

$d\mu\sim p\!\left(\frac{x-z}{\sqrt\sigma}\right)p\!\left(\frac{y-z}{\sqrt\sigma}\right)g(x,y,\sigma),\quad p(x)\sim e^{-x^2\!/2}.$

(В принципе, возможно рассмотреть и другие функции распределения $p(x)$

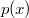
, например, равномерное на отрезке.) Ожидаемый ответ: улучшить точность по сравнению с обычным средним $(x+y)/2$

нельзя.

zykov · Сообщение **zykov** » 15 мар 2017, 12:48

peregoudov писал(а):Source of the post за счет отбрасывания "неподходящих" измерений

Этот момент не совсем ясен.

Если бы было не 2, а скажем 100, то можно было бы часть отбросить (что иногда и делают для крайних, конечно предполагая, что там не Гаусс).
А из 2 особо ничего не выбросишь.

peregoudov · Сообщение **peregoudov** » 15 мар 2017, 16:23

Нет, отбрасывается не одно из двух измерений. Отбрасывается вся пара целиком. У вас есть 100 пар измерений. (Причем все 100 раз могли измеряться разные величины.) Вы из них выбираете, скажем, 5 пар, и говорите: "вот для этих пяти пар я могу утверждать, что погрешность моей оценки в 5 раз лучше, чем погрешность отдельного измерения".

Ian · Сообщение **Ian** » 15 мар 2017, 21:40

peregoudov писал(а):...
В связи с этим напрашивается следующая постановка задачи. Пусть и --- две независимые случайные величины, распределенные по нормальному закону с одинаковой дисперсией $\sigma$ вокруг некоторого истинного значения . Пусть $f(x,y,\sigma)$ --- некоторая оценка истинного значения, а $g(x,y,\sigma)$ --- некоторый критерий отбора. Вопрос: как наилучшим образом выбрать и , чтобы "дисперсия по критерию" $\overline{(f-z)^2}$ была минимальной независимо от ? Усреднение производится по мере

$d\mu\sim p\!\left(\frac{x-z}{\sqrt\sigma}\right)p\!\left(\frac{y-z}{\sqrt\sigma}\right)g(x,y,\sigma),\quad p(x)\sim e^{-x^2\!/2}.$

Конечно, вопрос о наилучшей (в каком-то смысле) оценке среднего значения выборки очень подробно исследован, в любом учебнике читаем главы "Несмещенные оценки" и "Эффективные оценки". Поясню некоторые моменты, вдруг не повезет с учебником. Возьмем случайную величину с плотностью распределения

f_a(t)--у Вас это гауссова с известной дисперсией

\sigma и неизвестным матожиданием

a, поэтому именно это

a и фигурирует внизу как параметр. Рассмотрим выборку

(X_1,...X_n) как n-мерную случайную величину, компоненты которой независимы и каждая распределена по закону

f_a(t). Оценкой неизвестного параметра

a называется функция

\hat a(X_1,...X_n)-это уж так повелось, где про оценки, там крышки.У любой функции от многомерной величины с известным распределением также можно выразить распределение, короче,

\hat a(X_1,...X_n) является случайной величиной, распределение которой , правда, зависит от

a
Например, Вы не дискутируете такой способ оценивания (я про отдельные элементы, но можно было и про пары)
Отбросим наибольший элемент, как выпадающий из выборки. Но чтоб не было дискриминации, отбросим и наименьший.Потом снова повторим, и т.д, пока не останется только 1 или 2 элемента, если два, возьмем их среднее арифметическое. Определили оценку, которая называется выборочной медианой.Это пример того, что функция

\hat a(X_1,...X_n) не обязана задаваться конкретной формулой, а в сочетании с неким алгоритмом,который Вы обозначили

g.
Оценка называется несмещенной, если ее матожидание равно оцениваемому параметру, то есть для любого

a

E\hat a(X_1,...X_n)=a. Можно доказать, что выборочная медиана -несмещенная оценка. Даже иные более тупые оценки являются несмещенными, например,

\hat a(X_1,...X_n)=X_1-не смотрим никакое измерение, кроме первого.
Оценка называется эффективной, если она имеет наименьшую дисперсию в классе всех несмещенных. Видите, тут уже типа вариационной задачи -среди всех функций, удовлетворяющих данному линейному ограничению

E\hat a(X_1,...X_n)=a найти минимум функционала

E(\hat a(X_1,...X_n)-a)^2. И про это тоже есть теория, неравенство Крамера-Рао.
Значит, в самом оптимистическом варианте Вы придумали то, что есть в любом учебнике. Если оно так, то я потом продолжу.

peregoudov · Сообщение **peregoudov** » 15 мар 2017, 23:05

Коллеги, у меня опять такое ощущение, что вы не читаете сообщений. Нет никаких $n$

измерений, есть два измерения. После применения критерия отбора они не являются независимыми --- ну выписал же меру явно (я там dxdy забыл, ну, неважно). Так что Крамер-Рао не катит.

Придумал это все не я, это у заказчика завиральная идея. И вообще, я тем временем придумал простой примерчик, надеюсь, хоть он будет понятен.

Ну вот, набросал рисунок. Может быть, будет понятно даже и без слов.

Пусть распределение $x-z$

и

равномерное в интервале [-1,1]. Тогда совместное распределение равномерное в нарисованном квадрате. Возьму критерий $g(x,y)=\Theta(|x-y|-1.9)$ . Тогда мера у меня сосредоточена на выделенных серым треугольничках, а среднее (x+y)/2 по этой мере гораздо ближе к z, чем просто среднее по всему квадрату. Другое дело, что, желая выиграть в $n$

раз по точности, "подходящих измерений" остается $1/n^2$

от общего числа... И для нормального распределения этот трюк, вроде бы, не проходит...

Ian · Сообщение **Ian** » 16 мар 2017, 07:24

Так это я еще мягко сказал про Ваши сообщения а что скажет действующий преподаватель статистики они бывают очень эмоциональны из-за скудости языка статистики. Я всего 3 года ее преподавал и не совсем мое. Потом посмотрю

zykov · Сообщение **zykov** » 16 мар 2017, 08:00

peregoudov писал(а):Source of the post Тогда мера у меня сосредоточена на выделенных серым треугольничках, а среднее (x+y)/2 по этой мере гораздо ближе к z, чем просто среднее по всему квадрату.

Вопрос в том, какое среднее!
Дисперсия тем меньше, чем больше точек взято (при обычном усреднении). После фильтрации у Вас может быть и меньше дисперсия на одну точку, но точек то меньше стало.
Например у вас было 100 точек (или пар - не важно). Вы отфильтровали из них 20. Допустим дисперсия для этих 20 отфильтрованных меньше чем дисперсия для просто любых 20 (что логично при хорошем фильтре). Но скорее всего она будет больше, чем для усреднения по всем 100.

Тут дело в самом распределении.
Отбрасывание крайних (outliers) обоснованно, если распределение считается смесью хорошего распределения (типа Гаусса) и какого-то плохого. Например у Вас основное распределение даёт что-то типа Гаусса почти всегда, но изредка идут какие-то сбои и измерение выдаёт что-то совсем плохое (по неизвесто какому распределению, с большой дисперсией).

zykov · Сообщение **zykov** » 16 мар 2017, 08:09

Вот здесь нестыковка:

peregoudov писал(а):Source of the post Двумя приборами измеряется некоторая величина

и

peregoudov писал(а):Source of the post Пусть и --- две независимые случайные величины, распределенные по нормальному закону с одинаковой дисперсией $\sigma$ вокруг некоторого истинного значения

При таком предположении нет вообще никакого смысла в двух разных приборах. Просто берёте независимые измерения от одного прибора и усредняете. Можно и на пары разбить, но зачем?

Обычно два разных прибора вводят как раз потому что они разные.

peregoudov · Сообщение **peregoudov** » 16 мар 2017, 09:30

Так, я понял: абстрактные рассуждения доходят плохо. Давайте зайдем с другой стороны. Сделайте простой компьютерный тест.

1. Сгенерируйте 1000 пар независимых случайных чисел, равномерно распределенных на [-1,1]. Выберите секретное истинное значение (запишите на бумажке и никому не говорите). Прибавьте это значение к каждому из сгенерированных случайных чисел. Вы получите 1000 пар искусственно сгенерированных измерений. Дальше работаем только с этими измерениями, не зная истинного значения.

2. Тут можно идти двумя путями.

Первый путь. Для каждой пары вычисляем среднее. Получаем 1000 пар средних.

Второй путь. Для каждой пары применяем критерий: если модуль разности двух измерений из пары меньше 1.9, пару отбрасываем, в противном случае --- оставляем. Для всех оставленных пар вычисляем средние. Получаем сколько-то (как повезет) средних. Особо обращаю ваше внимание, что отбрасывание никак не опирается ни на истинное значение величины, ни на всю выборку в 1000 пар, а только и исключительно на результаты измерений из одной, текущей, пары (и на известную погрешность отдельного измерения).

3. Теперь проверяем, что у нас получилось. Берем истинное значение (то, которое записано на бумажке) и вычисляем среднеквадратичное уклонение полученных на шаге 2 средних от истинного значения. В первом пути --- всех 1000 средних, во втором --- всех оставленных средних. Сравниваем среднеквадратичные отклонения, полученные на первом и втором пути.

Мое предсказание: среднеквадратичное на втором пути будет значительно меньше.

peregoudov · Сообщение **peregoudov** » 16 мар 2017, 09:58

Персонально для Ian'а под катом.

peregoudov · Сообщение **peregoudov** » 22 мар 2017, 07:58

В общем, решил я изложить то, что уже давно посчитал, но все как-то было недосуг, а именно, теоретическое предсказание результатов машинного эксперимента.

Квадратичное уклонение вычисляется по формуле

$\overline{(f(x,y)-z)^2}= \frac{\int dx\,dy\,p(x-z)p(y-z)g(x,y)(f(x,y)-z)^2} {\int dx\,dy\,p(x-z)p(y-z)g(x,y)}.$

Заменой $x-z\to x$ , $y-z\to y$ в интегралах приводим к

$\overline{(f(x,y)-z)^2}= \frac{\int dx\,dy\,p(x)p(y)g(x+z,y+z)(f(x+z,y+z)-z)^2} {\int dx\,dy\,p(x)p(y)g(x+z,y+z)}.$

И тут напрашивается $g(x,y)=\tilde g(x-y)$ , $f(x,y)=(x+y)/2+\tilde f(x-y)$ , хотя, конечно, хотелось бы это получше обосновать. При таком выборе зависимость от $z$

пропадает

$\overline{(f(x,y)-z)^2}= \frac{\int dx\,dy\,p(x)p(y)\tilde g(x-y)((x+y)/2+\tilde f(x-y))^2} {\int dx\,dy\,p(x)p(y)\tilde g(x-y)}$

и напрашивается замена переменных $(x+y)/2=u$

,

$\overline{(f(x,y)-z)^2}= \frac{\int du\,dv\,p(u+v/2)p(u-v/2)\tilde g(v)(u+\tilde f(v))^2} {\int du\,dv\,p(u+v/2)p(u-v/2)\tilde g(v)}.$

Если еще немного сxулиганить, предположив, что $p(x)$

четная, то можно выкинуть перекрестный член

$\overline{(f(x,y)-z)^2}= \frac{\int du\,dv\,p(u+v/2)p(u-v/2)\tilde g(v) \left[u^2+\tilde f^2(v)\right]} {\int du\,dv\,p(u+v/2)p(u-v/2)\tilde g(v)}.$

Теперь видно, что $\tilde f$ только мешает, лучше всего положить ее равной нулю

$\overline{(f(x,y)-z)^2}= \frac{\int du\,dv\,p(u+v/2)p(u-v/2)\tilde g(v)u^2} {\int du\,dv\,p(u+v/2)p(u-v/2)\tilde g(v)}.$

Отсюда видно, почему я сфорулировал задачку про независимость $x+y$

и

: если

то мера в переменных $(u,v)$

факторизуется, а никакие ухищрения $\tilde g(v)$ не действуют. Проблема, однако, в том, что подобная факторизация происходит для одного-единственного $p(x)$

. Угадайте, для какого?

В общем же случае нужно исследовать дисперсию распределения

$q(u)=\int p(u+v/2)p(u-v/2)\tilde g(v)\,dv.$

Будучи записано через фурье-образы, квадратичное отклонение выглядит так

$\overline{(f(x,y)-z)^2}=- \frac{\int(\ln P(k))'' P^2(k)G(k)\,dk} {2\int P^2(k)G(k)\,dk}.$

Как это дальше проанализировать, пока не придумал.

zykov · Сообщение **zykov** » 22 мар 2017, 20:01

peregoudov писал(а):Source of the post В общем, решил я изложить то, что уже давно посчитал

А в чём смысл?

Аргумент, который я изложил чем-то не устраивает?

zykov писал(а):Source of the post Например у вас было 100 точек (или пар - не важно). Вы отфильтровали из них 20. Допустим дисперсия для этих 20 отфильтрованных меньше чем дисперсия для просто любых 20 (что логично при хорошем фильтре). Но скорее всего она будет больше, чем для усреднения по всем 100.

Просто есть такая эвристика, что для оптимальной оценки нужно учитывать всё, потому что даже какие-то далёкие точки несут дополнительную информацию, хотя и в меньшей степени. Лучше эту малую информацию учесть, чем выбросить.
Выбросить можно было бы по каким-то другим причинам. Например из соображений вычислительной эффективности, чтобы меньше считать, пусть и с потерей точности.

zykov · Сообщение **zykov** » 22 мар 2017, 20:07

Если нужен фильтр, то тут только один вариант.

g(x,y)=\tilde g(x-y), поскольку ничего неизвестно о среднем и система симметрична относительно сдвига.
Предикат будет

|x-y|<a с одним параметром

a, если плотность распределения убывает от центра (как для Гаусса) и нет каких-то там всплесков.
Остаётся только опеределиться с параметром

a. Чем меньше значение параметра, тем меньше дисперсия, но и тем меньше точек после фильтрации.

peregoudov · Сообщение **peregoudov** » 23 мар 2017, 08:07

zykov писал(а):Source of the post Аргумент, который я изложил чем-то не устраивает?

Вот этим

zykov писал(а):Source of the post Но скорее всего она будет больше, чем для усреднения по всем 100.

Я вам простой пример привел, когда это неверно.

zykov писал(а):Source of the post Если нужен фильтр, то тут только один вариант.

Не все так просто. Условием является оптимальность дисперсии по выборке. И, например, для $g(x,y)=e^{x+y}\tilde g(x-y)$ она тоже симметрична относительно сдвига. Но можно поставить условием, чтобы $g$

была характеристической функцией, то есть принимала только значения 0 и 1 (либо берем точку, либо не берем, "взять на 73%" при однократном измерении будет трудновато).

zykov писал(а):Source of the post Чем меньше значение параметра, тем меньше дисперсия

По-вашему, это не зависит от вида исходного распределения $p(x)$

? Но ведь, опять-таки, пример с нормальным распределением говорит об обратном. Да и последняя из моих формул подсказывает, что может быть и так и эдак.

Поэтому сейчас остается такая проблема: описать класс распределений $p(x)$

, для которых трюк с отбрасыванием понижает дисперсию, и как-то количественно охарактеризовать пригодность распределения к понижению дисперсии.

zykov · Сообщение **zykov** » 23 мар 2017, 11:25

peregoudov писал(а):Source of the post Я вам простой пример привел, когда это неверно

Можно ткнуть в этот пример?

peregoudov · Сообщение **peregoudov** » 23 мар 2017, 18:15

Вот

peregoudov писал(а):Source of the post Ну вот, набросал рисунок. Может быть, будет понятно даже и без слов.

Пусть распределение и равномерное в интервале [-1,1]. Тогда совместное распределение равномерное в нарисованном квадрате. Возьму критерий $g(x,y)=\Theta(|x-y|-1.9)$ . Тогда мера у меня сосредоточена на выделенных серым треугольничках, а среднее (x+y)/2 по этой мере гораздо ближе к z, чем просто среднее по всему квадрату.

zykov · Сообщение **zykov** » 24 мар 2017, 13:04

Хорошо, рассмотрим квадрат 2 на 2 вокруг неизвестного центра. Поправьте, если не прав, но видимо предполагается, что известно, что средние по

x и

y равны друг другу.

Для примера возмём 2000 точек. Каждая распределена вокруг неизвестного среднего равномерно в переделах от -1 до +1 (от среднего). Среднеквадратичное отклонение одной точки

\sigma^2=1/3.

Метод 1 оценки среднего: считаем среднее арифметическое по 2000 точек. Среднеквадратичное отклонение оценки

1/(3*2000)=1/6000.
Можно 2000 точек разбить на 1000 пар, посчитать среднее в каждой паре. Для среднего пары

\sigma^2=1/(2*3)=1/6. Усредяем эти средние по 1000 парам, получаем среднеквадратичное отклонение оценки

1/(6*1000)=1/6000. Тоже самое, никакой разницы.

Метод 2 оценки среднего: из 1000 пар отфильтровываем пары, у которых

|x-y|>1.9, считаем среднее для каждой пары из таких отфильтрованных пар, усредяем эти средние. Площадь фигуры отфильтрованных пар

0.1\cdot 0.1=0.01. Количество отфильтрованных пар - случайная величина, среднее которой

1000\frac{0.01}{4}=2.5. Т.е. в среднем где-то 2.5 пар получится после фильтрации. Средее арифметическое для каждой пары распределено также как среднее арифметическое для пар из маленького квадрата от -0.05 до +0.05 вокруг изначального среднего. Для среднего такой пары имеем

\sigma^2=1/(6*4*100)=1/2400.
Т.е. среднее одной отфильтрованной пары даёт более точную оценку, чем среднее просто любой пары. Видимо то, что Вы имели ввиду.
Но теперь мы усредяем это по всем отфильтрованным парам (в нашем случае это в среднем 2.5 пар) и получаем оценку среднего наших

x и

y. Для этой оценки будет

\sigma^2=1/(2400*2.5)=1/6000. Получается такая же точность, что и при методе 1.
Количество отфильтрованных пар - случайная величина. Если получится 3 или 4, то точность будет выше. Но может получится 1 или 2 пары, тогда точность будет ниже. А может и вовсе получится 0 пар после фильтрации, тогда никакой оценки вообще не будет.

peregoudov · Сообщение **peregoudov** » 27 мар 2017, 09:11

Вы неправильно считаете: не усредняете, а просто делите на общее количество исходов. А средние именно что различаются: 1/6 против 1/2400. Геометрически это очевидно (для того и рисовал картинку): применив критерий, вы от распределения по большому квадрату переходите к распределению по серым треугольничкам, что в отношении величины x+y (нарисуйте на картинке ее линии уровня) эквивалентно переходу к составленному из этих треугольничков маленькому квадратику со стороной в 20 раз меньшей, чем у большого.

zykov · Сообщение **zykov** » 27 мар 2017, 12:33

peregoudov писал(а):Source of the post А средние именно что различаются: 1/6 против 1/2400.

Да, различаются. Я про это написал.
А толку то? В конечном счёте всё равно и там, и там выходит отклонение

1/6000 (если у нас есть 2000 одиночных значений или 1000 пар).

Честно говоря тема достойна альт. раздела. Там обычно что-то такое толкают (вроде ВД).

peregoudov · Сообщение **peregoudov** » 29 мар 2017, 12:07

Не пойму, чем вы недовольны... Вы стартовое сообщение вообще читали? Ведь написано же русским по белому

peregoudov писал(а):Source of the post Не дают мне покоя мои "нефтяники". Теперь требуют, чтобы я развил идею, которая, на первый (да и на второй) взгляд, выглядит абсолютно бредовой.

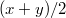
peregoudov писал(а):Source of the post Ожидаемый ответ: улучшить точность по сравнению с обычным средним нельзя.

Да, сумасшедшая идея, с которой мне нужно было разобраться. Идея не моя. Мне каким шрифтом это надо написать, чтобы вы, наконец, прочитали? У меня к ней исходно было скептическое отношение. Но у меня четкий принцип: нельзя называть что-то фигней, только потому, что моей левой пятке так показалось. Нужно разобраться. И лженаука, по моему глубокому убеждению, совсем не в том, что вы делаете неверные утверждения, а именно в том, что вы выносите вердикт, не желая разбираться в вопросе. Не утверждения имеют научный или ненаучный характер --- это бессмысленное словоупотребление. Научный или ненаучный характер имеет обсуждение этих утверждений.

В конце концов, если эта ветка вас так раздражает --- давайте ее удалим, мне не жалко.

Портал Естественных Наук, версия 1.1