Командный турнир

Ian · Сообщение **Ian** » 14 ноя 2021, 10:18

В прошлом году тоже был viewtopic.php?f=4&t=1387

: P1.jpg (102.27 KiB) 6734 просмотра

Дополнение: других кандидатов не было, каждый голос был отдан или за А, или за В

zykov · Сообщение **zykov** » 14 ноя 2021, 23:52

Можно для начала другую задачу решить. Найти вероятность 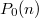$P_0(n)$

, что не было инверсий.
Тогда будет $P_1(n)=\sum_{k=1}^{n-1} \frac12 P_0(k) P_0(n-k)$ .

zykov · Сообщение **zykov** » 15 ноя 2021, 03:27

Как доказать - не знаю, но прямой расчёт для нескольких первых $n$

показал, что $P_0(n)=\frac{2}{n+1}$ .
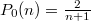Тогда, если не ошибся, будет $P_1(n)=\sum_{k=1}^{n-1} \frac{2}{(k+1)(n+1-k)}$ .
Явно посчитать сумму не вышло, но сначала эта вероятность растёт до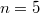 $n=5$

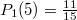, где $P_1(5)=\frac{11}{15}$ , а потом падает до нуля как $\frac{\ln n}{n}$ .

zykov · Сообщение **zykov** » 15 ноя 2021, 03:46

Моя формула с суммой для 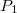$P_1$

не верна.
Посчитал напрямую вероятности для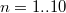 $n=1..10$

, вышло:
$0, \frac13, \frac25, \frac25, \frac{8}{21}, \frac{5}{14}, \frac13, \frac{14}{45}, \frac{16}{55}, \frac{3}{11}$

zykov · Сообщение **zykov** » 15 ноя 2021, 04:55

Удалось подобрать с помощью oeis A126079. Жаль, там нет описания, что это.
$P_1(n)=\frac{6\binom{2n+2}{n+1}-\binom{2n+4}{n+2}-8\binom{2n}{n}}{\binom{2n}{n}} = 4\frac{n-1}{(n+1)(n+2)}=\frac{12}{n+2}-\frac{8}{n+1}=6P_0(n+1)-4P_0(n)$

zykov · Сообщение **zykov** » 15 ноя 2021, 12:29

zykov писал(а):Source of the post Как доказать - не знаю, но прямой расчёт для нескольких первых показал, что $P_0(n)=\frac{2}{n+1}$ .

Это значит, что вероятность того, что только например первый всё время был лидером равна $\frac{1}{n+1}$ .
Всего количество вариантов $\binom{2n}{n}$ , значит количество вариантов, когда первый был лидером равно $\binom{2n}{n}/(n+1)$ .
А это число известно как Catalan number.

Возможно Third proof можно приспособить для $P_1$

.

Ian · Сообщение **Ian** » 15 ноя 2021, 12:33

Спасибо. Только формулы сегодня не читаются. Так как общее число вариантов

C^n_{2n}, достаточно считать число благоприятных вариантов среди них. Если добавить N(k,n) число благоприятных вариантов при старте из состояния (2k;0) то эти числа укладываются в треугольник паскаля но с граничными значениями немного другими. И любую предполагаемую формулу можно доказать через такой треугольник.

zykov · Сообщение **zykov** » 15 ноя 2021, 12:40

У меня формулы хорошо работают сейчас...
Попробуйте Ctrl-F5 нажать.

zykov · Сообщение **zykov** » 15 ноя 2021, 13:27

zykov писал(а):Source of the post Моя формула с суммой для не верна.

Да, там другая сумма должна быть.
$P_1(n) = \frac{2}{\binom{2n}{n}}\sum_{k=1}^{n-1} C_k \, C_{n-k}$
Так верно выходит.
Нужно только просуммировать.
Например используя Segner's recurrence relation $C_{n+1}=\sum _{i=0}^{n}C_{i}\,C_{n-i}$ .

zykov · Сообщение **zykov** » 15 ноя 2021, 20:59

Да. Так и есть.
То что $P_0(n)=2C_n / \binom{2n}{n}$ - очевидно. Один из случаев для числа Каталана (скобки например).
Если есть инверсия, то она происходить на голосе $m$

, где

нечётное от $3$

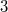до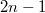

. Перед этим должна быть ничья.
Т.е. на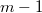 $m-1$

ничья, от

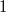до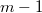

один лидер, от $m$

до

другой лидер. Количество вариантов для данного $m$

будет $2\, C_{\frac{m-1}{2}} \, C_{n-\frac{m-1}{2}}$ .
Значит $P_1(n) = \frac{2}{\binom{2n}{n}}\sum_{k=1}^{n-1} C_k \, C_{n-k}=\frac{2}{\binom{2n}{n}}(C_{n+1}-2C_n)=\frac{4(n-1)}{(n+1)(n+2)}$ .

Портал Естественных Наук, версия 1.1