Страница 1 из 1
О так называемой "задаче Деникина"
Добавлено: 26 окт 2021, 14:30
Таланов
О существовании задачи узнал из прессы. Будто бы Деникин (тот самый, Антон Иванович) единственный решил её, обучаясь в гимназии. В наши времена эту задачу предложил ученикам очень продвинутый директор очень продвинутого екатеринбургского лицея. Решил её тоже лишь один ученик плюс доцент некоего ВУЗа. Сам директор без очень высшей математики решить не может.
Формулировка задачи: чему равно среднее арифметическое всех хорд круга.
О так называемой "задаче Деникина"
Добавлено: 26 окт 2021, 14:35
zykov
Наверно "длин всех хорд".
У меня вышло - площадь круга поделить на диаметр круга.
О так называемой "задаче Деникина"
Добавлено: 26 окт 2021, 14:51
zykov
Достаточно рассмотреть только хорды перпендикулярные одному диаметру, т.к. из симметрии - для любого другого диаметра всё будет тоже самое.
Если эти хорды падают равномерно, то средняя длина будет:
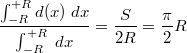
О так называемой "задаче Деникина"
Добавлено: 26 окт 2021, 14:51
Таланов
Предлагалось такое решение. Статмоделирование не подтверждает его правильность.
О так называемой "задаче Деникина"
Добавлено: 26 окт 2021, 14:54
Таланов
zykov писал(а):Source of the post Достаточно рассмотреть только хорды перпендикулярные одному диаметру
Видимо этого недостаточно. Видимо какие-то хорды всё-таки не учитываются.
О так называемой "задаче Деникина"
Добавлено: 26 окт 2021, 15:11
zykov
Не в этом дело.
Дело в том, как распределены случайные хорды.
Я тут имел ввиду, что просто бросаем случайно прямую на плоскость. Если она пересекает окружность, то считаем условное матожидание длины этой хорды. Если правильно провести статмоделирование этой ситуации, то всё сойдётся.
Но можно и другую трактовку предложить. Случайно бросают две точки на окружность и ищут матожидание длины этой хорды. Из симметрии, можно зафиксировать одну точку и бросать только вторую точку.
Тут тоже просто:
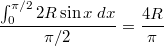
О так называемой "задаче Деникина"
Добавлено: 26 окт 2021, 15:24
Таланов
О так называемой "задаче Деникина"
Добавлено: 26 окт 2021, 16:16
Ian
Есть доказательство, найти ошибку.
Вероятность того, что две произвольные хорды в круге пересекутся, меньше 1/2
Зафиксируем одну хорду, которая делит окружность на дуги а и b. Вероятности попадания концов другой хорды на них обозначим P(a)+P(b)=1
Вероятность пересечения [math]2P(a)P(b)\leq \frac 12, причем равенство только если хорда-диаметр, а это с вероятностью 0
О так называемой "задаче Деникина"
Добавлено: 27 окт 2021, 03:16
zykov
Исходная формулировка задачи безграмотная.
"среднее арифметическое всех хорд круга" - бессмысленно.
Надо говорить о матожидании длин хорд. А для этого надо задать распределение.
Я вот только два естественных варианта показал. Наверно можно ещё придумать.
Первый вариант мне больше нравится, т.к. решение выглядит красиво. Такие рассуждения про площадь в духе интегрального исчисления ещё в древности проводили, когда самого интегрального исчисления ещё не было.
Тут хорда рассматривается, как пересечение некой прямой и окружности. При этом берётся, что прямые на плоскости располагаются равномерно. Все углы наклона равновероятны (равномерно по углу). Среди параллельных прямых с одним наклоном они тоже имеют равномерную плотность распределения.
Второй вариант - это если рассмотреть хорду как отрезок между двумя точками на окружности и потребовать, чтобы эти точки были равномерно распределены вдоль окружности. Даже ещё проще конструкция. Просто взять интеграл вдоль окружности. Может тоже можно как-то на пальцах сделать, чтобы явно интеграл не считать.
О так называемой "задаче Деникина"
Добавлено: 27 окт 2021, 03:22
zykov
Ian писал(а):Source of the post Вероятность того, что две произвольные хорды в круге пересекутся, меньше 1/2
Ian, тут же тоже надо задать вид распределения хорд.
Вы всё правильно посчитали по "второму варианту", когда хорда - отрезок между двумя точками, которые равномерно распределены по окружности.
Но есть и другие варианты. Например можно попробовать оценить это же по "первому варианту".
О так называемой "задаче Деникина"
Добавлено: 27 окт 2021, 04:14
zykov
zykov писал(а):Source of the post Например можно попробовать оценить это же по "первому варианту".
Попробовал посчитать, вышло ровно
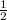
.
О так называемой "задаче Деникина"
Добавлено: 27 окт 2021, 10:21
Ian
Я претендовал на то, что доказательство не зависит от вида распределения.То есть P(a) может быть не пропорциональна длине дуги а, а получаться как-то сложно. Но она существует, и значит, такое неравенство. Ошибка там рядом. При разных способах попадания в а и b могли оказаться не независимы и [math]P(a,b)>P(a)P(b)
О так называемой "задаче Деникина"
Добавлено: 27 окт 2021, 14:53
zykov
Не уверен, что понял о чём речь.
Если это "второй вариант", то очевидно что
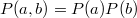
.
Если это "первый вариант", то очевидно что обычно
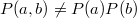
.
О так называемой "задаче Деникина"
Добавлено: 28 окт 2021, 20:23
peregoudov
О так называемой "задаче Деникина"
Добавлено: 29 окт 2021, 03:00
zykov
Тут вообще не верно.
"b=2*(0.5-ran())" - это

меняется от -1 до 1 только если угол ноль. Иначе оно будет менятся в более широких пределах. Крайний случай - это касательная под этим углом. Т.е. должно быть "b=2*sqrt(1+a^2)*(0.5-ran())".
Если моделировать "первый случай", то выбираем равномерно угол от
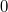
до
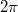
- угол наклона перпендикуляра к хорде. Выбираем равномерно высоту хорды
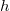
от
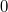
до
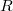
. Длина хорды будет
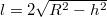
. Не зависит от угла.
Если моделировать "второй случай", то совсем просто. Угол
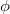
между концами хорды распределен равномерно от
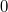
до
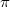
. Длина хорды будет
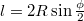
.
Я вот подумал тут. Хотя задача и не сформулирована чётко, но всё же "первый случай" логичнее второго. По условию "хорды распределены равномерно", что соответствует "первому случаю". А "второй случай" - это "концы хорд равномерно распределены по окружности". В условии концы вообще не упоминаются.
О так называемой "задаче Деникина"
Добавлено: 29 окт 2021, 13:56
peregoudov
В первом случае как раз возможно геометрическое решение "без интегралов", нужно только увидеть, что ответ равен отношению площади круга (тот самый интеграл) к диаметру. Во втором случае геометрическая интерпретация сложнее, это длина циклоиды (катим круг, а хорда --- между фиксированной точкой круга и мгновенной осью вращения). Вот только не знаю, умели ли древние длину циклоиды вычислять без интегралов.