Сумма ряда из рекурсий
Добавлено: 21 янв 2021, 10:01
Ian

- 24xn.jpeg (26.28 KiB) 6872 просмотра
Формула для суммы получается
[math]\frac {24}{x_1-1}, но как доказать
Сумма ряда из рекурсий
Добавлено: 21 янв 2021, 16:34
zykov
Обозначим
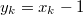
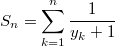
Тогда
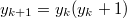
.
Отсюда
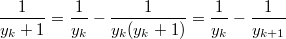
Получим телескопическую сумму:
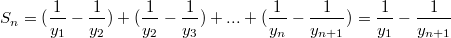
Сумма ряда из рекурсий
Добавлено: 22 янв 2021, 12:49
Ian
Действительно, если функция [math]f(n) такова, что существует [math]F(n)\to 0:F(n)-F(n+1)=f(n), то сумма ряда [math]\sum_1^{\infty}f(n)=F(1). У нас [math]F(n)=\frac 1{x_n-1},\;f(n)=\frac 1{x_n}.
Пытаюсь подобрать f ,F чтобы условие представляло собой удобное но сложное рекуррентное уравнение, получится генератор олимпиадных задач для 1 курса 1 семестра, что ценно, их не так много существует)
Сумма ряда из рекурсий
Добавлено: 22 янв 2021, 15:06
zykov
Да, здесь можно обобщить.
Так, если сделать замену
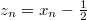
, то рекурентное отношение будет
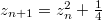
. Т.е. получим
квадратичную динамическую систему в центрированном виде с
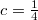
. Например используют для демонстрации
фрактала Джулия.
Можно составить сумму
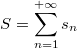
, где
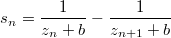
с каким-то параметром

.
Если привести к общему знаменателю, то будет квадратный многочлен деленный на кубический многочлен.
Но только при параметрах
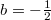
и
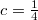
этот кубический многочлен делится без остатка на этот квадратный и получается красиво.
(Там остаток равен
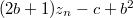
.)
Сумма ряда из рекурсий
Добавлено: 22 янв 2021, 22:07
zykov
Это просто значит, что
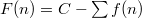
.
Т.е. если есть формула для конечной суммы (как например для геометрической или арифметической прогрессий), то из неё можно соорудить телескопическую сумму.