Решение для m=4 как "Number of palindromic structures using a maximum of four different symbols" здесь http://oeis.org/A007581
Оно еще и просто выводится. Рассмотрим [math]- число разбиений n различимых предметов на 4 неразличимых ящика (пустые ящики допускаются). Расположение n-го предмета даст 4 различных способа тогда и только тогда, когда 4 ящика с n-1 предметами различимы. Если в этом расположении пустых ящиков было не более одного, то все ящики различимы (один, может быть, отличим от остальных тем, что он пуст). Если пустых ящиков два, то два положения n-го предмета неразличимы и для [math] расположений будет три принципиально различных места поместить n-й предмет вместо 4-х. А для одного из указанных (когда все предыдущие n-1 предмета в одном ящике) всего 2. Получаем
[math]
Это обычная линейная неоднородная рекуррентность
[math], что совпало с формулой в oeis
Для произвольного, но фиксированного m, общая формула, видимо, нереальна, но какова асимптотика по n (при фиксированном m)?
Если бы ящики были различимы, ответ разумеется [math]
Комбинаторика: n различимых предметов в m неразличимых ящиков
Комбинаторика: n различимых предметов в m неразличимых ящиков
Да так наверно и будет 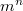 .
.
Вот возмите какое-то (например
(например 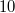 ) и случайно распределите гораздо большее количество различимых предметов
) и случайно распределите гораздо большее количество различимых предметов  (например
(например 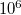 ) в эти
) в эти  различимых ящиков. С подавляющей вероятностью, не будет двух ящиков с одинаковым количеством предметов. Значит количество этих комбинаций с различимыми ящиками для одной комбинации с неразличимыми ящиками равно количеству перестановок -
различимых ящиков. С подавляющей вероятностью, не будет двух ящиков с одинаковым количеством предметов. Значит количество этих комбинаций с различимыми ящиками для одной комбинации с неразличимыми ящиками равно количеству перестановок - 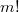 .
.
Т.е. асимптотика будет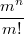 .
.
Вот и у Вас тут асимптотика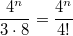 .
.
Вот возмите какое-то
Т.е. асимптотика будет
Вот и у Вас тут асимптотика
Комбинаторика: n различимых предметов в m неразличимых ящиков
Отлично. А если бы предметы были неразличимы такая вот жуть https://ru.wikipedia.org/wiki/Разбиение_числа
Кто сейчас на форуме
Количество пользователей, которые сейчас просматривают этот форум: нет зарегистрированных пользователей и 2 гостей